1.1.1 Понятие за бройна система
Concept notation
Всяка човешка дейност е свързана по особен
начин с абстрактното понятие количество. Читателят вероятно има спомени
от ранното детство, когато всеки един от нас бавно и с много труд е усвоявал
разбирането за това какво е “едно”, “две”, “три” и т.н. и
още, че “две” и “две” прави “четири” и прочие достатъчно много и
достатъчно сложни правила, свързани с количествата изобщо.
В древните общества са се
употребявали специални изрази, които са означавали при необходимост например “три
лодки”, ”две риби”, “десет пръста” и пр., но не е
съществувало отвлечено (абстрактно) понятие (разбиране) “три”, “две”
или “десет”. Предаването на съобщения за числеността на елементите в
едно множество, например група хора, е наложило формирането на някаква
общоприета (стандартна) съвкупност, най-често от части на човешкото тяло – две
ръце, четири крака, двадесет пръста, ... Когато броят на елементите в такива
групи не достигали, се формирали други групи – от пръчици, от раковини, от
камъчета, от възелчета и др. подобни. Така в процеса на развитие се е
преминавало по необходимост към преброяване на вече създадените групи (от
двойки, от десятки, от дузини, ...), което е правело разбирането за количество
все повече и повече отвлечено от предметната му същност. Вероятно по това време
са били общоприети определени (характерни и полезни) количества, които днес
можем да наречем елементарни или възлови. Заедно с това неизбежно
са се появили и зачатъчните аритметични правила и е започнало познаването на
все повече количества.
Съвкупността от тези знания
изграждат една крайно необходима ни система, наречена бройна система.
Тя е предназначена да представя (означава) поясненото по-горе понятие количество.
Процесът на образуване в едно общество на подобна система е изключително
сложен. Бройната
система е една от най-старите абстракции на човешкия род, тъй като тя е
част от основата на човешките отношения, при което е съставна част на
съответния разговорен език. Цялата оценъчна система на човека се изгражда в
процеса на обучение до автоматизъм от ранното му детство в продължение на много
години върху някаква бройна система.
Всяка бройна система може да се определи строго като система изградена от три съвкупности:
· Съвкупност от
елементарни количества и символи за тяхното означаване;
· Съвкупност от
правила за изобразяване на произволни количества;
· Съвкупност от
правила за опериране с количествата или още числата.
Символите за означаване на
елементарните количества се наричат цифри. Смисълът или разбирането за
елементарните количества човек възприема и заучава обикновено в процеса на
обучение в ранните си години. В зависимост от правилата за изобразяване
бройните системи се определят като позиционни и непозиционни. Тези наименования
ще бъдат изяснени по-късно тук.
Бройните системи са
възниквали (създавани) във всяка отделна човешка общност и понеже те са били
разделени както териториано, така и във времето, системите са твърде различни.
В древен Египет например битували няколко бройни системи.
В една от тях елементарните количества, за които е имало писмени симвили, са
били съответно следните:
![]()
В различните етапи на развитие на тази древна цивилизация са се появявали и други символи. При изписване на дадено число символите били подреждани хоризонтално. Еднаквите символи можели да се групират, а записите изразявали предимно натурални числа. Така например числата от естествения ред се означавали както следва:
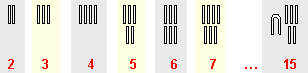
В асиро-вавилонската
писменост са използвани такива символи, които е било удобно да се нанасят върху
меките и неизсъхнали глинени плочки, които по това време служели като траен
документ.
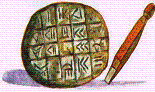
Символите били два вида клиновидни
отпечатъци, които са разчетени и днес се разбират по следния начин: вертикален
клин ![]() означава единица (1)
или всяка степен на числото 60 (600=1, 601=60, 602=600, ...); ъглов клин
означава единица (1)
или всяка степен на числото 60 (600=1, 601=60, 602=600, ...); ъглов клин ![]() означава десет (10).
Системата за изобразяване на числата била позиционна по организация.
Вертикалните клинове можели да се подреждат в групи. В една група можело да се
разполагат до 10 ъглови клина, при което с такива групи означавали следните
количества:
означава десет (10).
Системата за изобразяване на числата била позиционна по организация.
Вертикалните клинове можели да се подреждат в групи. В една група можело да се
разполагат до 10 ъглови клина, при което с такива групи означавали следните
количества:

Ъгловите клинове можели да се разполагат в групи до 5 и с такива групи означавали количествата:
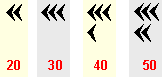
Символите и групите от символи се
подреждали в хоризонтална последователност според съвременните ни представи за
запис на число. Изразяваното с една последователност от такива символи и групи
количество се прочита като еквивалент в познатата ни 10-чна бройна система по
аналогичен начин. По този начин се разчита показаната по-долу символна
последователност:
![]()
Интересно е да се спомене, че в тази
бройна система не е познат символ за празна позиция, което не гарантирало
винаги правилното прочитане на числото.
Както може да се види от
горния запис и от множеството примери, дадени по-долу, независимо от посоката в
която се пишело в дадена писменост (отляво надясно или обратно), естествено е
било записите на числата да започват със “старшите” цифри, т.е. със
старшите позиции. В другия край на записа обикновено се намирали “младшите”
цифри или “младшите” позиции. Това неписано правило обикновено определяло и
начина за прочитане на числото. В този смисъл може да се твърди, че има няколко
системи за представяне на едно число – писмен, говорима, жестоматична и др.
В древна Гърция
по времето на първия известен математик Талес (624–574 г. пр. н.е.) се
използвала атическата система за записване на числата. Отделните числа били
означавани с първите букви от наименованията им. Например: P (пенте – 5); D (дека – 10); H (екатон – 100); C (хилиой – 1000); M (мириой – 10000).
Тази ситема е известна от трудовете гръцкия граматик Херодиан и по времето на
Перикъл (V век пр. н.е.), Херодиановите знаци станали официална система за
записване на числата. Ето някои примери
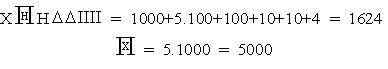
По същото време, в друг гръцки град –
Милет (гръцка малоазийска колония Йония), за означаване на числата използвали
всички букви от азбуката, като поставяли над тях отличаващ знак, например
“тилда” ~ . Тази
система е известна като Йонийска номерация. Архимед и Аполоний са записвали
изчисленията си в Йонийска система. В град Атина Йонийската система била
възприета през III век пр. н.е. Ето ка са изглеждали тогавашните числа

Следващото изображение се нарича кипу.

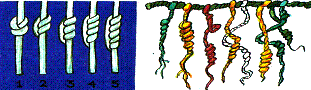
Изобразените връвчици “кипу” се
използвали от древните инки за представяне на числата. Кипу представляват
сложни плетеници от връвчици и възли, направени върху тях, изпълнени с различен
брой намотавания. Връвчиците се изработвали или от вълна на лама или от памук.
Намирани са кипу с до 2500 връвчици. Този вид “писменост” се използвал преди
всичко като финансов израз на данъчни отчети, отчитал се броят на животните или
количеството на урожая. Тази писменост не е разчетена напълно. Приема се, че
по-голяма част от изразената числена информация е в десетична бройна система,
но има и алтернативна хипотеза за някакво подобие на двоичната бройна система.
Исторически използването на кипу също е спорно – от 3000 години преди н.е. до
700 години от н. е.
Следващата картинка представя
по какъв начин древните маи са изобразявали числата.
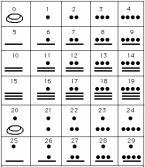
Създаването през IX век на славянската
писменост от братята Кирил и Методий е силно повлияно от гръцката
азбука. Пренесен бил начинът за означаване на числата чрез използване на
буквите от азбуката.
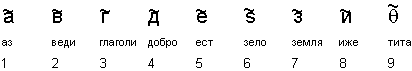
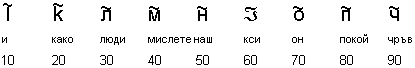
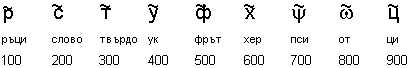
При тези означения на възловите числа последователността ![]() изобразява числото
изобразява числото
![]() .
.
Знакът ![]() , който е поставен в началото, означава хиляди. В
славянската номерация не е използвана буквата “буки”, тъй като гръцката буква
“бета” съответства на две славянски – “буки” и “веди”. Съществували са и други
символи, например за числото 103 се употребявал
символът
, който е поставен в началото, означава хиляди. В
славянската номерация не е използвана буквата “буки”, тъй като гръцката буква
“бета” съответства на две славянски – “буки” и “веди”. Съществували са и други
символи, например за числото 103 се употребявал
символът ![]() - (тысяча); за
числото 106 - символът
- (тысяча); за
числото 106 - символът ![]() - (тьма);
за числото 1012 - символът
- (тьма);
за числото 1012 - символът ![]() - (легеон)
и др.
- (легеон)
и др.
В римската
бройна система символите за означаване на цифрите също изминали своя път на
еволюция от ранните етруски символи (етруски - жители на днешна Италия през
VII-VI век пр. н.е.) до съвременните: I, V, X, L, C, D, M, които означават следните
количествата съответно.
|
M |
D |
C |
L |
X |
V |
I |
|
1000 |
500 |
100 |
50 |
10 |
5 |
1 |
Въпреки че тези символи приличат на някои
букви, техният произход няма нищо общо с азбуката, а по-скоро с жестоматичната
система I – палец; V – ръка; X – две ръце и т.н.
Етруските използвали повече знаци, но римляните се задоволили само със седем
знака. С тяхна помощ било възможно записването на всяко цяло число от 1 до
4999. Основните правила за изписване на произволни числа
могат да бъдат обобщени така:
·
Символът за единица I се използва
съвместно само със символите V и X;
·
При записване на числата всеки от символите I, X, C
и M може да се повтаря
до 3 пъти;
·
Всеки символ, намиращ се отдясно на друг символ, който има
по- голяма стойност, се прибавя към тази стойност. Например VI се чете 5+1=6. Символът за единица може да се повтаря до 3
пъти, например VIII изразява 5+1+1+1=8;
·
Всеки символ, намиращ се отляво на друг символ с по- голяма
стойност, се изважда от тази стойност. Например IV се чете 5-1=4;
·
По същия начин символът X може да се постави вляво от символа L или символа C, а символ C - вляво от
символите D или M;
·
Символите са групирани в низходящ ред по стойност, освен
тези за които се прилага предишното правило. На практика това правило гласи, че
при римските цифри първо се изписват хилядите, после стотиците, след това
десетиците и накрая единиците. Има се предвид писане отляво надясно;
·
Символ, представляващ стойност кратна на 10 (10х), не може
да се поставя пред (т.е. отляво на) символ, по-голям от 10x+1. Така например M може
да бъде предшестван от D и C, но не
и от I, V, X или L.
Според правилата за
изразяване на произволно количество следва да се получи сумата от еквивалентите
на цифрите в последователността. Така например последователността MMDLXXXII следва да изразява
количеството
MMDLXXXII = 1000+1000+500+50+10+10+10+1+1 = 2582.
Символите D и M първоначално са
били изписвани с помощта на вертикална черта или малки скоби. Например записът I ) можел да замести символа D, а записът ( I )
- символа M. Тази система е
позволявала числа по-големи от 1000 да се изписват чрез увеличаване на броя на
скобите. Така например 10 000 се е изписвало така (( I )), а 100,000 така ((( I ))). Римляните не са имали име за 1,000,000 и рядко са
използвали числа от такъв размер.
В Индия
в началото на новата ера широко била разпространена говорима позиционна
десетична система за номериране, в която имало няколко синонима за означаване
на нулата. Тази система е прародител на съвременната десетична бройна система.
От VIII век тази система започва да се разпространява в източно арабските
цивилизации - Персия. Познанията за аритметичната теория на числата се
разпространявали бавно и преди всичко чрез трудовете на арабските математици,
един от които е бил ал-Хорезми (абу Джафар Мохамед ибн Муса ал-Ховаризми,
живял през VIII-IX век). Ал-Хорезми написал ръководство за числата (“Китаб Аль-джебр валь-мукабала”), което било преведено на латински език и оказало
силно влияние на Леонардо Пизански (Фибоначи), който от своя страна през
1202 година написал научен труд по аритметика. Той пък от своя страна изиграла
решаваща роля за разпространение на индоарабските числа в Европа.
Необходимостта от все повече
количествени означения развивали бройните системи, познанията за числата и
математиката в крайна сметка. Исторически е известно например, че на Архимед му
се е налагало да убеждава своите съвременници, че може да бъде посочено число,
което е по-голямо от “броя на песачинките в света”. За измерванията са
били необходими означения и за части от елементарните количества. По тази
причина дробните числа били известни в Египет и Вавилон. В началото на новата
ера в Китай и в Индия са познавали всички аритметични операции над дробните
числа. В съвременната позиционна система дробите били въведени за първи път от
неизвестен математик, който се подписвал с името ал-Уклидиси
(“Евклидов”). В написания от него в Дамаск трактат по аритметика бил използван
знакът ‘
като десетична запетая. Трактатът на ал-Уклидиси не станал известен. Така около
5 века по-късно, в началото на 15-ти век, десетичните дроби били преоткрити от
известния математик и астроном ал-Каши (Джемшид бен-Масуд ед-Дин ал-Каши,
починал около 1436-та година). В началото на XV век ал-Каши, като първи
директор на астрономическата обсерватория в Самарканд, написал книгата “Поучения
за окръжността”, в която между другите нови резултати въвежда и десетичните
дроби.
В Европа най-ранните от известните примери
с десетични дроби е открит в текст от XV век, където числото 153,5 се умножава
с числото 16,25 и в отговор се получава числото 2494,375, което в текста било
наречено “турски метод”. Десетичните дроби се разпространили след отпечатването
през 1585-та година на книгата “Десета” от холандеца Симон Стевин. Преди
това европейците представяли цялата част на числата в десетична бройна система,
а дробната – в 60-чна или като обикновена дроб (отношение).
Тук ние няма да се задълбочаваме повече върху историческото изучаване на произхода, същността и развитието на различните бройни системи. Читателят вероятно разбира, че те са различни, защото са създавани от различни цивилизации, разделени една от друга както териториално, така и във времето. В днешно време ние използваме в различна степен елементи от древните бройни системи. Например за обикновено номериране използваме римската система, за означаване на ъглови градуси и време – вавилонската. Надяваме се обаче краткото изложение да провокира у читателя интерес към самостоятелно изследване в това направление.
Според правилата за
изразяване на произволно количество, бройните системи могат да се класифицират
в две основни групи
·
Непозиционни. В такива системи поставянето на даден символ в
различните позиции на записа на числото е еднакво относно неговия принос към
общото количество. Изразеното от една символна последователност количество се
определя от специално формулирани в бройната система правила;
·
Позиционни. В тези системи правилата за изобразяване на
произволно количество са такива, че отделните позиции в последователността от
символи не са равностойни относно приноса им в общото количество. Това
означава, че един и същи символ ще променя количествения си вклад в общото
количество при поставянето му в различни позиции.
В обществата исторически първо се
появявали непозиционните системи. Техен общ недостатък представлява трудността за
запис на големите числа. Представянето на големите числа изисква много дълъг
запис или много голям набор от символи за означаване на възлови количества. При
непозиционните системи този недостатът е принципен. Тези системи се развивали и
усъвършенствали или били заменяни от по-съвършенните позиционни системи.
Трудността в позиционните системи се систои в необходимостта от дефиниране на
означения за теглата на позициите. Тъй като въвеждането на безкрайна азбука за
означаване на теглата е невъзможно, то най-често това се постига с някаква
математическа функция, позволяваща изчисляване на теглото на дадена позиция
чрез нейния номер и теглата на останалите позиции. Така поради универсалността
и удобството на правилата си позиционните бройни системи се считат за
по-съвършенни.
Преди обаче да пристъпим към строгото представяне на тези
“по-съвършенни” системи, трябва да признаем, че темата, по която беседваме,
няма да бъде изчерпана с написаното тук. Темата за бройните системи, и въобще
за системите, с които може да се представи количествената информация, е много
по широка и в това читателят ще може да се увери, запознавайки се с написаното
и в останалите раздели на тази книга. Систематизираното изложение на темата
може да се намери в научната литература, с която читателят ще следва сам да
работи, съобразявайки се единствено със своето любопитство.
Математиката и в частност
онази област, която наричаме “теория на числата” е била вдъхновение за много
математици и инженери да изследват и да разработват различни бройни системи,
търсейки тяхното ефективно използване в компютърните системи. Такива системи
например са:
· Системи с числа на Фибоначи;
· Системи с числа на Мерсен;
· Знако-разрядни системи;
· Иерархически системи;
· Системи в остатъчни класове;
· Позиционно-остатъчни системи;
· Знако-разрядни позиционно-остатъчни системи;
· Модулно-логаритмични системи
· И др.
С други думи авторът
препоръчва на читателя да гледа на изложеното в тази книга като на основа,
върху която продължава процеса на развитие в областта на компютърните науки,
защото както е писал през 17-ти век великият Лайбниц (Gottfried Wilhelm
Leibniz – 1646-1716):
Който иска да се ограничи с настоящото,
без да познава миналото,
той никога няма да го разбере.
Всички известни позиционни бройни системи се определят като адитивно-мултипликативни. Позиционният принцип за представяне на числата се оправдава от следната теорема:
Нека
![]()
представлява последователност от естествени числа, различни от единица. Тогава за всяко естествено число А може да бъде намерено едно и само едно естествено число n, за което уравнението
![]()
има решение в цели (естествени) числа
![]() ,
,
такива че
![]()
При това, уравнение (1.1.1.1) се удовлетворява само от една единствена наредена последователност (кортеж)
![]()
от цели числа, удовлетворяващи условията (1.1.1.2). Този кортеж може да се приеме за единствен запис на числото А в адитивно-мултипликативна бройна система с коефициенти
![]() .
.
В така определената система всяка цифра на числото допринася за формиране на общото количество в такава степен, каквото е теглото на позицията в която е поставена. Според (1.1.1.1) теглото Qk на k-тата позицията се определя от произведението на коефициентите q, както следва
![]() .
.
При тези означения, записът например на десетични цифри в една последователност (7259) с тегловни коефициенти 12, 10, 8 и 1 ще означава следното число
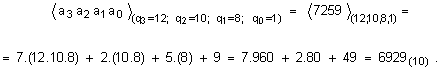
По силата на тази теорема,
бройна система, в която
![]() ,
,
и целите числа
![]()
могат да бъдат само измежду числата ![]() , наричаме бройна с основа q или просто q–ична
бройна система. Според това определение, числото q съответства на броя на цифрите ak (на елементарните количества) и се нарича основа на
бройната система. Специално с буква r ще означим най-голямото по стойност за
бройната система елементарно количество:
, наричаме бройна с основа q или просто q–ична
бройна система. Според това определение, числото q съответства на броя на цифрите ak (на елементарните количества) и се нарича основа на
бройната система. Специално с буква r ще означим най-голямото по стойност за
бройната система елементарно количество: ![]() . Употребяваната в живота днес система е десетичната бройна система.
В тази система са дефинирани 10 елементарни количества, означавани със
символите 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, чиито смисъл и стойност познаваме
добре.
. Употребяваната в живота днес система е десетичната бройна система.
В тази система са дефинирани 10 елементарни количества, означавани със
символите 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, чиито смисъл и стойност познаваме
добре.
В подкрепа на твърдението, че десетичната бройна система е добре позната и че тя е удобна, използваема и универсална, е наличието на специални означения на характерни количества. Наименованията на тези количества, част от които прилагаме в следващата таблица, могат да формират изговарянето на твърде голям брой произволни числа.
|
Позиция |
Полином |
Стойност |
Наименование |
|
0 |
100 |
1 |
единица |
|
1 |
101 |
10 |
десетица |
|
2 |
102 |
100 |
стотица |
|
3 |
103 |
1000 |
хиляда |
|
6 |
106 |
1 000 000 |
милион |
|
9 |
109 |
1 000 000 000 |
милиард (билион) |
|
12 |
1012 |
1 000 000 000 000 |
трилион |
|
15 |
1015 |
1 000 000 000 000 000 |
квадрилион |
|
18 |
1018 |
1 000 000 000 000 000 000 |
квинтилион |
|
21 |
1021 |
1 000 000 000 000 000 000 000 |
секстилион |
|
24 |
1024 |
1 000 000 000 000 000 000 000 000 |
сентилион |
За всяко естествено число E, записано чрез последователност от m цифри на дадена q–ична бройна система, е в сила теорема, която твърди че то, подобно на (1.1.1.1), може да се представи по единствен начин със следния полином
![]()
където
коефициентите на полинома са съответните цифри на числото. Така например
записът
![]()
ще означава
десетичното количество
![]()
Едно произволно в съвременния смисъл
количество, различно от елементарните, се означава с наредена последователност
от знак, цифри и разделител
![]()
която се нарича число.
Разделителят (,) формира две части на числото – цяла
и дробна. При тези условия числото има следния полиномен вид,
който съответства на определението (1.1.1.1) и (1.1.1.4):
![]()
където с буква а е означена съответната
цифра от азбуката на системата, с буква i – номерът на позицията, в която тя стои, а
с буква q –
основата на бройната система. Количеството qi се нарича тегло на позицията с
номер i.
Числата се изобразявали за да
може да се оперира с тях. Най-естественото, първичното опериране е обобщението
на две и повече количества. Обобщението или обединяването е естествено явление
в живота, а заедно с него върви отделянето. Така може да твърдим, че
първичната операция е операция събиране на две количества (числа).
Всички останали операции са производни на нея, т.е. се определят чрез
нея. Днес тези операции наричаме аритметически.
Операция
аритметическо събиране е винаги определена. Тя, както и останалите
аритметически операции, се дефинира таблично. Операция аритметическо изваждане
е определена (т.е. възможна) само когато умалителят е по-малък от умаляемото.
От казаното следва, че операция умножение е винаги определена. Операция деление
не е определена ако делителят е равен на нула. Изчерпателно изложение на
правилата за опериране ще бъде представено в следващи раздели.
Следващият раздел
е:
1.1.2 Преобразуване на
числа от една бройна система в друга
(Convert numbers from one notation system to another)