1.1.2 Преобразуване на числа от една бройна
система в друга
Convert numbers from one
notation system to another
А) Преобразуване на цели числа
Ще разгледаме класическата
необходимост да изобразим познато ни десетично число в друга известна ни позиционна
бройна система с основа q,
така щото да е в сила равенството
![]()
Това преобразуване се нарича право.
Нека числото Х се представя в двете бройни системи според (1.1.4) както следва:
![]()
![]()
където q е
известната основа на бройната система, в която търсим еквивалентното
изображение на числото Х. Тук се предполага, че q-ичната бройна система е
известна. За този еквивалент не са известни коефициентите на неговия полином bi и техния брой n.
Нека изпълним в познатата ни 10-чна бройна система делението:
![]()
Тъй като приемаме b0 за цифра от q-ичната бройна система, то b0 < q, което ще рече, че b0 е първият остатък от делението на числото Х с
основата q. Частното Х1 е цяло число.
Изпълняваме
следващото деление
![]()
при което се вижда, че b1 е следващият остатък. Полученото частно е Х2.
Ако
последователно продължим да делим частните – Х2, Х3, Х4, и т.н. ,
![]()
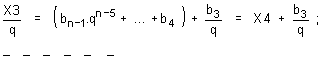
последователно ще получаваме остатъците b2, b3, b4, и т.н.
Процесът на това последователно деление ще завърши с получаване на частното
![]()
Нулевото частно означава, че коефициентът bn-1 е последният. При това можем да приемем, че получената
последователност от остатъци, подредени в обратен ред, представя търсения
q-ичен еквивалент, т.е. можем да запишем равенството
![]()
Описаният
изчислителен процес може да се характеризира като циклически с предварително
неизвестен брой повторения. Условието за неговото прекратяване е получаване на
поредно частно равно на нула. Няма никакво съмнение обаче, че такова частно ще
бъде получено след краен брой итерации. Ето защо това преобразование се
нарича точно. В резултат на него се определят цифрите на търсения
еквивалент и техният брой. Разбира се q-ичното число се записва чрез символите
на q-ичните цифри, избрани за означаване на елементарните количества в
системата – [0,1,2, ... ,(q-1)]. Крайният алгоритъм на това преобразуване можем да
изкажем така:
Изходното цяло число и последователно получаваните в процеса
частни се делят с основата на желаната бройна система (записана като число в
изходната бройна система) многократно и последователно до получаване на поредно
частно нула.
Търсеният еквивалент се изразява чрез получените при
деленията остатъци, записани в обратен на получаването им ред. Остатъците,
представляващи цифрите на еквивалента, се записват със съответните им символи
според кодовата таблица на желаната бройна система
Задачата
за намиране на десетичния еквивалент на зададено q-ично число е обратна
на представената по-горе и преобразованието с право се нарича обратно.
Намирането на десетичния еквивалент се постига с помощта на полинома (1.1.2.2)
когато всички означени в него действия се изпълнят според правилата на 10-чната
бройна система. Например нека е зададено 16-чното число F2A7(16) . Намираме 10-чният му
еквивалент така:
![]()
Вижда се, че в полиномния запис на числото основата на бройната система както и всички цифри на 16-чното число са заместени със своите 10-чни еквиваленти, които са известни по условие. Крайният алгоритъм на това преобразуване можем да изкажем така:
Изходното число се представя в полиномен вид, в който коефициентите
и основата на бройната система са записани като числа в желаната бройна
система.
Изпълняват се означените в полиномния запис на изходното
число действия, но според правилата на бройната система в която желаем да
преминем.
Надяваме
се, че читателят не би се затруднил да обобщи изложените решения за по-общия
случай на преобразуване между две бройни системи с произволни основи
![]() .
.
Б) Преобразуване на дробни числа
Дробните числа (или
поточно правилните дроби) могат да се разглеждат като съставна част от общия вид
(1.5) на едно произволно число. Имайки предвид отрицателните степени на
полиномния запис на тези числа, преобразуването им не може да се извърши чрез
описаната по-горе схема. Ще разгледаме правото преобразование
![]() .
.
Нека десетичното число Х е
правилна дроб, т.е.
![]()
Ще търсим q-ичния еквивалент на
числото във вида
![]()
Ако не всички цифри bi в последователността са равни на
най-голямото елементарно количество r=(q-1), то е изпълнено следното отношение:
![]()
![]()
Полученият в скобите израз
представлява безкрайна геометрична прогресия. Имайки сумата от нейните
елементи, горното отношение се изяснява до вида
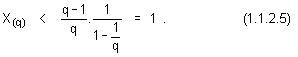
Умножаваме двете страни на
равенство (1.1.2.4) с основата на бройната система q и получаваме
![]()
Съгласно доказаното по-горе
неравенство (1.1.2.5) следва, че цялата част на числото X.q е числото b-1, а Х1 е дробната му част.
Ако
постъпим по същия начин с правилната дроб Х1, ще получим аналогичен резултат:
![]()
в който коефициентът b-2 представлява цялата му част.
Ако
последователно продължим да умножаваме правилните дроби – Х2, Х3, Х4, и т.н.,
![]()
![]()
ще получаваме последователно целите числа b-3, b-4, b-5, и т.н. Процесът на това последователно
умножение ще завърши ако се получи правилна дроб Xk=0. В
този случай се казва, че преобразованието е точно. За съжаление тази
ситуация формално не е гарантирана предварително. Обикновено процесът на
умножение е безкраен, тъй като Xk¹0. В
такъв случай последователните умножения следва да се прекратят след получаване
на достатъчен брой цифри b-k. Броят на цифрите в търсения еквивалент се приема за достатъчен, ако той е
представен с точност не по-малка от тази на изходното десетично число. В този
случай се говори, че преобразованието е неточно, т.е. разчита се на X(10) » X(q) в определена степен. При записване на приблизителното
равенство може да бъде приложена и функцията за закръгляне round(X,v) , която
ще бъде пояснена по-късно в глава 3 на тази книга.
В
резултат на описания последователен процес доказахме, че цифрите на търсеното
q-ично число се получават като цели части на числата ( q.Xi, i=1,2,3, … , j ), което ни дава право да запишем
![]()
Описаният
изчислителен процес може да се характеризира като циклически с предварително
неизвестен брой повторения. Условието за неговото прекратяване е получаване на
поредно произведение с нулева дробна част. Ако това условие не се изпълнява,
цикълът се прекратява след определяне на достатъчен брой цифри в търсения
еквивалент. Разбира се q-ичното число се записва чрез символите на q-ичните
цифри, избрани за означаване на елементарните количества в системата – [(0,1,2,
... ,(q-1)]. Крайният алгоритъм на това преобразуване можем да изкажем така:
Изпълняват се последователни умножения на изходното дробно
число, или дробните части на последователно получаваните в процеса
произведения, с основата на желаната бройна система, до получаване на поредно
произведение равно на нула или до достигане на необходимата за еквивалента
степен на точност.
Търсеният еквивалент се изразява чрез последователността от целите
части на получените при умноженията произведения, записани като цифри, според
кодовата таблица на желаната бройна система.
Описаното преобразование е
неточно в общия случай. Записваният еквивалент е неточен. Съдържащата се в него
грешка е принципна и не може да бъде отстранена. Тя може само да бъде намалена
чрез удължаване на неговия запис.
Задачата
за намиране на десетичния еквивалент на зададена q-ична правилна дроб е обратна
на представената по-горе, а преобразованието се нарича обратно. Намирането
на десетичния еквивалент се постига с помощта на полинома (1.1.2.4) когато
всички означени в него действия се изпълнят според правилата на 10-чната бройна
система. Например нека е зададено 16-чното число 0,F2A7.
Намираме 10-чният му еквивалент така:
![]()
= 0,9375 + 0,0078125 + 0,00244140625 + 0,0001068115234375 =
0,9478607177734375(10)
Вижда
се, че в полиномния запис на числото, основата на бройната система, както и
всички цифри на 16-чното число, са заместени със своите 10-чни еквиваленти,
които са известни по условие (според кодовата таблица). Изчисляването на
търсения 10-чен еквивалент обаче е свързано с изчислението на тегловните
коефициенти на полинома, които са степени с отрицателен показател. Това
означава, че тегловните коефициенти се изчисляват в общия случай по формулата
за реципрочната стойност 1/qi ,
която не гарантира точно изчисление на часното, т.е. на тегловните коефициенти.
Това в крайна сметка означава, че търсеният десетичен еквивалент ще бъде
получен неточно. Тук ние ще се задоволим с този общ извод и няма да се
впускаме в изследване на признаците за делимост, които имат място при някои
бройни системи. Тази задача оставяме на любознателния читател. В случаите,
когато преобразованието е неточно, точността на търсения еквивалент се постига
в смисъла на предварително известната степен на точност, както беше казано
по-горе в правата задача.
Крайният алгоритъм на това преобразуване можем да изкажем така:
Изходното число се представя в полиномен вид, в който коефициентите
и основата на бройната система са записани като числа в желаната бройна
система.
Изпълняват се означените в полиномния запис на изходното
число действия, но според правилата на бройната система в която желаем да
преминем.
Описаното преобразование е неточно в общия случай. Записваният еквивалент е
неточен. Съдържащата се в него грешка е принципна и не може да бъде отстранена.
Тя може само да бъде намалена чрез удължаване на неговия запис.
Надяваме
се, че читателят не би се затруднил да обобщи изложените решения за по-общия
случай на преобразуване между две бройни системи с произволни основи
![]() .
.
В)
8-чна и 16-чна бройни системи
Бройните системи с основа 8 и 16
са позиционни. Ще разгледаме тези системи, тъй като те представляват определен
интерес по ред причини, които тук няма да изтъкваме. Системите се определят на
пъво място чрез символите на своите елементарни количества. Общо прието е за
тази цел да се използват символите на 10-чната бройна система с тяхната еквивалентна
стойност, а в 16-чната система, да бъдат допълнени със съответните латински
букви, както е представено в следващите кодови таблици:
Таблица 1.1.2.1
Кодова таблица на 8-чната бройна система
|
Символи (цифри) на бройната
система: |
Двоична стойност (еквивалент) |
Десетична стойност
(еквивалент) |
|
0 |
000 |
0 |
|
1 |
001 |
1 |
|
2 |
010 |
2 |
|
3 |
011 |
3 |
|
4 |
100 |
4 |
|
5 |
101 |
5 |
|
6 |
110 |
6 |
|
7 |
111 |
7 |
Таблица 1.1.2.2
Кодова таблица на 16-чната бройна система
|
Символи (цифри) на бройната
система: |
Двоична стойност
(еквивалент) |
Десетична стойност
(еквивалент) |
|
0 |
0000 |
0 |
|
1 |
0001 |
1 |
|
2 |
0010 |
2 |
|
3 |
0011 |
3 |
|
4 |
0100 |
4 |
|
5 |
0101 |
5 |
|
6 |
0110 |
6 |
|
7 |
0111 |
7 |
|
8 |
1000 |
8 |
|
9 |
1001 |
9 |
|
A |
1010 |
10 |
|
B |
1011 |
11 |
|
C |
1100 |
12 |
|
D |
1101 |
13 |
|
E |
1110 |
14 |
|
F |
1111 |
15 |
Преобразованията на числа от
една бройна система в друга се подчиняват на вече изложените по-горе методи.
Допълнителен интерес тук представлява особенната връзка на тези бройни системи
с двоичната, ето защо отделно разглеждаме преобразованията:
![]()
Като
начало ще обърнем внимание на факта, че основата на тези бройни системи може да
се изрази чрез степенна функция при основа 2, т.е. 8=23 и съответно 16=24 .
В-1) Преобразуване на цели числа
Ще разгледаме преобразуването на цели 8-чни числа в двоична бройна система. Нека приемем, че двоичният еквивалент на изходното 8-чно число е известен. Според (1.1.2.2), двоичното число се представя от своя полином така:
![]()
Алгоритъмът за преобразуване,
синтезиран по-горе в пункт А), изисква да се извършват последователни деления
на изходното число и в последствие на получаваните частни, с основата на
бройната система, в която желаем да преминем (записана като число в изходната
бройна система), както следва:
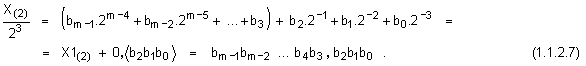
Вижда се, че остатъкът от
делението е 3-битовият кортеж от младшите цифри на двоичното число.
Следователно можем да го приемем за двоичния еквивалент на съответната осмична
цифра, според кодовата таблица на осмичната бройна система. Ако например ако
![]()
то според общо приетата кодова таблица на 8-чната система 1.1.2.1, това е
осмичната цифра 5, т.е.
![]()
При следващото аналогично
деление ще получим следващия 3-битов остатък:
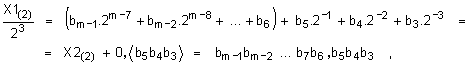
който по аналогичен начин можем да заместим с осмична цифра:
![]()
Този циклически процес
продължава, докато се получи поредно частно нула. В края на процеса се
получават n на брой
3-битови кортежи. Търсеният еквивалент се записва с цифрите на 8-чната бройна
система (кодова таблица 1.1.2.1):
![]()
Анализирайки описаното
преобразуване, в крайна сметка стигаме до извода, че вместо да изпълним
фактически необходимия брой операции деление, можем да формираме последователно
върху двоичното число 3-битовите кортежи, които ще ни позволят лесно да запишем
търсения осмичен еквивалент. Единственото правило, което следва да спазваме е,
че формирането на кортежите трябва да извършваме от младшите в посока на
старшите разряди, както е показано на следната рисунка:
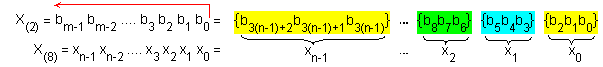
Правейки този извод, естествено
и лесно се досещаме за следващия извод, че обратното преобразование на едно
8-чно число в двоична бройна система може да се изпълни като всяка негова 8-чна
цифра бъде заместена с 3-битовия си двоичен кортеж (код) според кодовата
таблица 1.1.2.1. Обикновено 3-битовият кортеж се нарича триада.
Продължавайки
в същия дух на обобщение стигаме до заключението, че преобразуването на цели
16-чни числа в двоична бройна система се подчинява на горе изложения процес и
на направените изводи. Разликата е в това, че след деление с числото 24 аналогично
на (1.1.2.7), в дробната част на частното ще се получи 4-битов кортеж. В крайна
сметка търсеният 16-чен еквивалент се записва като k разряден кортеж от 16-чни цифри аналогичен на
(1.1.2.8), но според кодовата таблица 1.1.2.2:
![]()
Обратното преобразование, от
16-тична в двоична бройна система, се извършва също по аналогичен начин, но
чрез заместване на 16-чните цифри с техните 4-битови двоични кортежи
(еквиваленти), според кодовата таблица 1.1.2.2. Обикновено 4-битовия кортеж се
нарича тетрада.
Остана да представим преобразуването на цели числа от 8-чна бройна система в 16-чна и обратно. Тези две преобразования могат да се извършат по метода представен по-горе в пункт А), но отчитайки функционалната връзка в основите на бройните системи и направените току що изводи, лесно стигаме до заключението, че алгоритъма на този метод може да не се прилага фактически и преобразованията да се извършат значително по-лесно, чрез прилагане на схемите (1.1.2.8) и (1.1.2.9). Бихме могли да изразим казаното по-лесно чрез следните две схеми (за право и обратно преобразуване):

От (1.1.2.10) се вижда, че и
двете преобразувания се извършват като за междинна бройна система се използва
двоичната. Не се извършва никакво деление, а само заместване на цифрите и
кортежите, според кодовите таблици 1.1.2.1 и 1.1.2.2.
Схемата (1.1.2.10) е достатъчно обща за да твърдим че тя изразява всички възможни между разглежданите бройни системи преобразования.
В-2) Преобразуване на дробни числа
За да направим по-бързо и по-лесно своите изводи сега ще разгледаме най-напред преобразуването на двоични дробни числа в 8-чна бройна система. Приемайки двоичното число за дадено, според (1.1.2.4) то се представя от своя полином така:
![]()
Алгоритъмът за преобразуване,
синтезиран по-горе в пункт Б), изисква да се извършват последователни умножения
на изходното число и в последствие на получаваните в произведенията дробни
части, с основата на бройната система, в която желаем да преминем (записана
като число в изходната бройна система), както следва:
![]()
Вижда се, че в цялата част на
полученото произведение е формирана от трите старши двоични цифри на изходното
число, т.е. ефектът от умножението се е изразил само в преместване на запетаята
на 3 бита надясно. Тъй като цялата част на така полученото произведение не може
да надхвърля стойността на множителя, т.е. числото, представено от 3-битовия
кортеж, е винаги по-малко от основата на бройната система 8, то за тази бройна
система стойността на кортежа е елементарно количество, което може да бъде
изразено чрез съответния символ според кодовата таблица 1.1.2.1. С други думи
можем да запишем, че
![]()
При следващото аналогично
умножение ще получим произведението:
![]()
в цялата част на което стои следващият 3-битов кортеж, който от своя страна
представлява следващата 8-чна цифра:
![]()
Този циклически процес
продължава, докато се получи поредно произведение с нулева дробна част. Че
такава ще се получи следва от това, че изходното дробно число има краен запис.
В резултат на този процес се получават n на брой 3-битови кортежи и търсеният 8-чен еквивалент се
записва с цифрите на 8-чната бройна система (виж кодовата таблица 1.1.2.1)
както следва:
![]()
Анализирайки описаното
преобразуване в крайна сметка стигаме до извода, че вместо да изпълним
фактически необходимия брой операции умножение, можем да формираме върху двоичното
число 3-битовите кортежи, които ще ни позволят лесно да запишем търсения
осмичен еквивалент. Единственото правило, което следва да спазваме е, че
формирането на кортежите трябва да извършваме от старшите в посока на младшите
разряди, както е показано на следната рисунка:
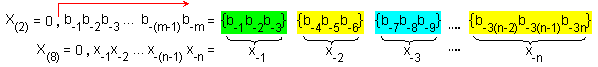
Обратното преобразование, от
8-чна в двоична бройна система се извършва също по аналогичен начин, но чрез
заместване на 8-чните цифри с техните 3-битови двоични кортежи (еквиваленти),
според кодовата таблица 1.1.2.1.
Правото
и обратното преобразования между двоична и 16-тична бройни ситеми се изпълнява
по аналогичен начин, но кортежите са 4-битови и заместването им е според
кодовата таблица 1.1.2.2 :
![]()
Всички възможни преобразования на дробни числа между 2-чна, 8-чна и 16-чна бройни системи могат да се представят чрез следната схема:
![]()
Тази схема се отличава от
аналогичната (1.1.2.10) само по посоката, в която се извършва
формирането на кортежите.
От смесването на двете схеми (1.1.2.10) и 1.1.2.14) се получава схема, по която може да се преобразуват в трите бройни системи произволни числа.
Г)
Алгоритми за машинно преобразуване на бройната система
Изложените по-горе (точка А, Б и В) алгоритми за преобразуване на числа от една бройна система в друга обикновено се използват при ръчно изпълнение. Алгоритмите са тривиално следствие от математическото определение на понятието бройна система. За съжаление машинната им реализация не винаги е възможна. Това е така по много причини, които предстои тепърва да изясняваме. На този етап можем да изтъкнем например невъзможността да представим непосредствено символите за означаване на цифрите на числата; изпълнението на аритметическите действия е определено в различните бройни системи по различен начин; и не на последно място това са изискванията към тяхното бързодействие и ефективната апаратна (техническа) реализация.
Машинно
реализуемите алгоритми за преобразуване на бройната система и съответните им
апаратни структури ще бъдат изложени в глава 3
на тази книга,
а тяхната числена илюстрация може да бъде видяна в книга [2].
Следващият раздел е:
1.1.3 Избор на бройна
система за реализация на цифрови изчислителни устройства
(Choice
notation system of implementation in digital processors)