3.2.5.2
Алгоритъм
на Леман (Lehman)
Algorithm
of Lehman
Алгоритъмът,
който ще бъде
изложен тук,
е известен
още като
усъвършенстван
алгоритъм на
Бут.
Основната
идея,
заложена в
този алгоритъм,
произтича от
недостатъците
на алгоритъма
на Бут и е
насочена
срещу тях.
Същността й
се състои в
предложението
за анализ не
само на
текущия
разряд на
множителя, но
и на
съседните
отляво разряди
така, че
определянето
на
необходимата
за
изпълнение в
текущия такт
операция да бъде
обвързано и
съобразено с
бъдещата операция.
Ето защо към
двойката
разряди (yi, yi-1),
разглеждани
на всеки такт
при
алгоритъма на
Бут, сега се
добавя и
следващият
отляво разряд
yi+1, с което
се формира
тройката (yi+1, yi, yi-1),
която се
подлага на
анализ в
текущия такт.
От всички 8 комбинации,
които могат
да се появят
в тези три
разряда,
най-интересни
са онези,
които според
алгоритъма
на Бут, определят
две
последователни
аритметически
операции,
както е
показано на
следните ситуационни
схеми:
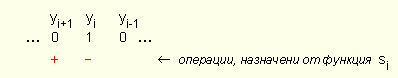
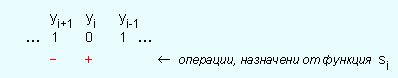
Според
алгоритъма
на Бут, както
е показано в
горните
ситуационни
схеми, в текущия
i-ти
разряд може
да бъде
назначена
операция събиране
или
изваждане.
Тази
операция обаче
може да бъде
заменена на
противоположната
в следващия
такт, ако се смени
стойността
на цифрата на
множителя,
т.е. ако има преход
от 1 в 0 или от 0 в 1.
Тази
ситуация
означава, че
дължината на
групата от
последователни
единици в
множителя е
равна на 1.
По
същество, в
зависимост
от цифрите на
множителя (yi+1, yi),
според
алгоритъма на
Бут в такива
случаи се
натрупват
следните
суми:
·
За първата
схема: ( -Мн +
2.Мн ) ;
·
За втората
схема: (
+Мн - 2.Мн ) .
Разгледани резултантно, тези суми имат следните стойности:
·
За първата
схема: ( -Мн +
2.Мн ) = +Мн ;
·
За втората
схема: (
+Мн - 2.Мн ) = -Мн ,
което
означава, че
вместо да се
изпълняват назначените
според
алгоритъма
на Бут две операции:
събиране и
след това
изваждане за
първата
схема, или
изваждане и
събиране за
втората
схема, с
междинно
изместване
след първата
операция, то
в текущия такт
може да бъде
изпълнена
резултантната
операция с
последващо
изместване.
Изказаният извод относно възможността за замяна на двойката последователни операции с една, представлява по същество оптимизацията на алгоритъма на Бут. Казаното може да се илюстрира върху същите две схеми:


С
други думи,
ако бъде
разпозната
една от горните
две схеми, в
текущия i-ти такт
следва да се
изпълни
операция,
която се
определя от
следващия (i+1)-ви бит
на множителя.
Разпознаването на текущата комбинация от цифри на множителя и назначаването на съответната операция в алгоритъма на Леман се реализира с помощта на логически функции, аналогично дефинирани на тези в алгоритъма на Бут - (3.2.5.1.2). Логиката обаче на тези функции е друга, а именно: в текущият такт ще се изпълнява само изместване, ако според алгоритъма на Бут се назначава операция, но в предидущия такт също е била изпълнена операция, а когато трябва да се изпълни операция, тя се определя от следващата цифра на множителя, т.е.
![]()
Алгоритъмът
на Леман с
успех се
прилага и върху
числа
представени
в
допълнителен
код. В тези
случаи, така
както и в
алгоритъма на
Бут, в
умножението
участва и
знаковата цифра
на множителя.
В края на
умножението,
когато в
най-младшия
разряд на
регистъра на множителя
yi=(РгМт’[0]) се окаже
знакът на
множителя, в
случай, че функцията
ci
назначава
операция,
последната не
може да се
определи от
цифрата,
съдържаща се
в лявостоящия
разряд (РгМт’[1])![]() yi+1, тъй като
към този
момент тази
цифра не принадлежи
на множителя.
Цифрата в
този разряд
на регистъра
на множителя
е най-младшия
бит на
междинната
сума. Така в
този
последен такт,
ако се налага
да се извърши
операция, тя
се определя
от цифрата на
знака на
множителя.
В резултат на
това
съждение
окончателният
вид на
логическите
функции на
отместването
ci и на
операцията si в
алгоритъма
на Леман е
следният:
yi+1, тъй като
към този
момент тази
цифра не принадлежи
на множителя.
Цифрата в
този разряд
на регистъра
на множителя
е най-младшия
бит на
междинната
сума. Така в
този
последен такт,
ако се налага
да се извърши
операция, тя
се определя
от цифрата на
знака на
множителя.
В резултат на
това
съждение
окончателният
вид на
логическите
функции на
отместването
ci и на
операцията si в
алгоритъма
на Леман е
следният:
![]()
където
EQ е
флагът за
нулево
съдържание
на БрЦ., т.е.
индексната
променлива i в
горната
формула е
достигнала
последното
си значение n-1.
При
тези
логически
функции
ситуационната
схемата за
умножение с
множителя Y=10101=21
ще има
следния вид:
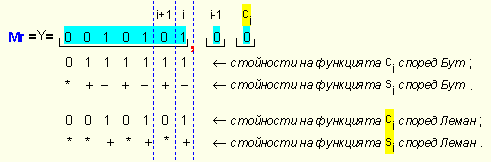
в резултат на която се получава произведението Z = X.Y = X.(1 + 4 + 16) = X.21.
В тази
схема, за
определяне
на
стойността на
функцията на
изместването
ci в
най-младшия
разряд, се
взема нулева
начална
стойност на
същата
функция - c0=0, тъй
като тази
логическа
функция,
според уравнението
(3.2.5.1.4), има времеви
характер, т.е
нейната
текуща
стойност
зависи от
стойността й
в предидущия
момент. В този
случай
индексната
променлива i
означава
освен номера
на текущия
бит и номера
на текущия
такт. От това
следва, че за
да се
реализира
алгоритъма
на Леман в
базовата
логическа
структура от
фигура 3.2.2.1.1 (или
от фигура 3.2.2.2.1) към
регистъра на
множителя РгМт
са
необходими два
допълнителни
тригера - един за
съхраняване
на
обработения
вече разряд
на множителя yi-1 - (РгМт[-1]) и
един за
съхраняване
на текущата
стойност на
функцията на
изместването
ci - (Tc).
Тъй като тази
функция изменя
стойностите
си синхронно
с изместванията
на множителя,
то нейният
тригер
трябва да има
структурата
на тригерите,
реализиращи
изместващия регистър
на множителя,
т.е.
двутактов,
двуетажен RS-тригер.
Началното
установяване
на този тригер
следва да се
определи в
съответствие
с началната
стойност на
функцията на
отместването.
По-долу
на фигура 3.2.5.2.1 е
показана
част от
принципната
логическа схема
за
реализация
на функциите
на Леман (горната
част на
регистъра на
множителя РгМт’’
и на
споменатите
тригери не са
изобразени).
Показаните
управляващи
сигнали
между двете
нива УС14 и УС16
са
взаимствани
така както са
дефинираните
за
структурата
от фигура 3.2.2.1.1.
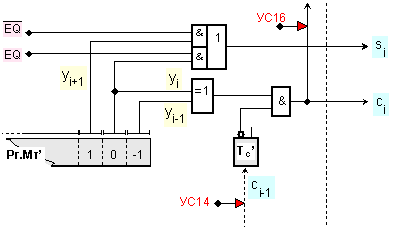
Фиг. 3.2.5.2.1.
Логически
функции на
Леман
Както
може да се
види от
ситуационната
схема за
определяне
на
стойностите
на функциите ci и si в
алгоритъма
на Леман,
показана
по-горе за множителя
Y=21, в процеса на
умножение
могат да се
назначат
последователно
няколко
еднакви
операции, при
които
вероятността
за
препълване в
процеса на
натрупване е
напълно
реална. Вече
беше казано,
че при препълване
възниква
проблемът с
разрушаване
на знака на
междинната
сума, ето
защо за
неговото
отстраняване
в алгоритъма
на Леман, за
микрооперация
аритметическо
изместване
надясно,
отново
трябва да се
приложи логическата
функция за
неговото
възстановяване
(3.2.3.4), или
модифициран
допълнителен
код за
представяне
на
междинната
сума.
Алгоритъмът
на Леман може
да бъде
реализиран в
логическа
структура,
която се
получава от
базовата
логическа
структура за
умножение по
метода с
младшите
разряди
напред. Измененията,
които трябва
да се
направят в
нея, са много
малка част от
общите
апаратни
разходи и
вече бяха
пояснени.
По-долу
представяме микропрограмата
за
функциониране
на устройство
за умножение
по
алгоритъма
на Леман,
базирано на
структурата
от фигура 3.2.2.1.1. Тя
не се
различава
съществено
от представената
в предидущия
параграф за
алгоритъма
на Бут.
Отличията са
нищожни, а те
се отнасят до
следното: в
началния
момент е
необходимо
тригерът на
функцията на
изместването
ci да бъде
установен в
нулево
състояние. За
целта следва
да се
използва
управляващият
сигнал УС17.
Броячът на
цифрите
трябва да приеме
за начална
стойност
числото n и
при всяко
изместване
надясно в
знаковия
разряд на
междинната
сума – РгСМ[n-1]
да се приема
стойността
на
възстановяващата
знака
функция S.
Алгоритъмът
на Леман може
да се прилага
върху числа
представени
в
допълнителен
код, при
което
произведението
се получава автоматично
в същия код. С
други думи
алгоритъмът
на Леман
отстранява
недостатъка
на
алгоритъма
на Бут, но от
своя страна
въвежда свои
недостатъци,
един от които
е загубата на
хомогенността,
която
притежава
алгоритъмът
на Бут.
Микропрограмата
за умножение
по
алгоритъма
на Леман в
модифицираната
базова
логическа
структура от
фигура 3.2.2.1.1 има
следния вид:
0:: Начало // Текст
на
микропрограма
за умножение
по алгоритъма
на Леман
на
числа
представени
в допълнителен
код // ;
1::
УС2 :
РгМн :=0 , УС6 : БуфРг :=0 , УС10 :
РгХ :=0 , УС21 : РгСМ :=0 ,
УС13 :
ТП := 0 ,
УС17 : РгМт’’ :=0 , УС17 : ТргС’’ := 0 , УС15 : РгМт’[n-1¸-1] := 0 , УС15 : ТргC’ := 0 ,
УС23 : БрЦ := n ;
2::
УС1 :
РгМн := ШД=Мн ;
3::
УС7 :
РгМт’ := ШД=Мт ;
4:: Ако ( ci ) то // следва
операция //
{ Ако ( si ) то //
следва
операция
изваждане //
{ УС5 :
БуфРг := not(РгМн) ,
УС8 :
ТП := 1 = +1СМ ,
УС21 :
РгСМ := 0 , УС17 : РгМт’’ := 0 ,
УС17 : ТргС’’ := 0 } ;
иначе //
следва
операция
събиране //
{
УС4
:
БуфРг := (РгМн) ,
УС13 : ТП
:= 0 ,
УС21 :
РгСМ := 0 , УС17 : РгМт’’ := 0 } ; }
//
изместване //
5::
УС20 :
РгСМ[n-1] := S , УС19 : РгСМ[n-2 0] := СМ[n-1 1] ,
УС18 :
РгМт’’[n-1] := СМ[0] ,
УС16 : РгМт’’[n-2 ¸ -1] := (РгМт'[n-1 ¸ 0]) , УС16 :
ТргС’’ := ci , УС22 : БрЦ := (БрЦ)-1 ;
6::
УС9 :
РгХ := (РгСM) , УС14 : РгМт’ := (РгМт’’) ,
УС14 : ТргС’ := (ТргС’’) ;
7:: Ако ( not(EQ) ) то { Премини
към 4:: } ;
8:: Край ;
Както
вече за много
предходни
раздели сме отбелязвали,
така и за
този ще
отбележим, че
читателят
може да
намери
множество
числени
примери,
илюстриращи
представения
алгоритъм в книга [2].
Следващият
раздел е:
3.2.5.3
Умножение с
два разряда
едновременно
(с младшите
разряди
напред)
( Multiplication with two bits at the same time (with the juniors ahead) )