3.2.8
Деление на
числа в
допълнителен
код
Division twos complement numbers
В
случаите,
когато
операндите X и Y са числа
със знак,
представени
във форма с фиксирана
запетая, те
са в
допълнителен
код, ето защо
е необходимо
да се
разгледа
възможността
за
изпълнение
на операция
деление в
допълнителен
код. Освен
това тук ще
разглеждаме
възможността
за
реализация
на
алгоритъма за
деление в
допълнителен
код върху
базовата
логическа
структура от фигура 3.2.6.3.
Като се има
предвид
изложената
теоретична
постановка
на тази
операция,
алгоритъмът
за деление не
се различава
съществено
от този в прав
код.
Измененията
се отнасят до
правилото (3.2.6.14), според
което се
определя
поредната
цифра в
частното и
следващата
операция.
Според
това правило
в прав код за
тази цел е
достатъчно
да се
анализира
само знакът
на текущия
частичен
остатък Rm. В
допълнителен
код обаче
поради
вероятността
от различно
съчетание на
знаците на остатъка
и делителя,
за осмисляне
на текущия
резултат само
знакът на
частичния
остатък не е
достатъчен.
Поредната
цифра в
частното
трябва по
същество да
отразява
дали
делителят се
е съдържал в
нормализирания
частичен
остатък, а всяка
следваща
операция
трябва да се
избира така,
че редицата
от частични
остатъци да
се схожда към
нула. За тези
две цели е необходимо
знакът
на текущия
частичен
остатък да се
тълкува в
зависимост
от знака на
делителя.
Аналогичните
правила за
деление без
възстановяване
на частичния
остатък в
допълнителен
код, се
изразяват
най-лесно в
табличен вид
(виж таблица
3.2.8.1)
Таблица 3.2.8.1
Определяне
на цифра в
частното и операцията
|
Знак на остатъка Rm |
Знак на делителя W |
Поредна
цифра в
частното zm |
Следваща
операция Rm+1= |
|
+ |
+ |
1 |
2. Rm -
W |
|
+ |
- |
0 |
2. Rm +
W |
|
- |
+ |
0 |
2. Rm +
W |
|
- |
- |
1 |
2. Rm -
W |
От
таблицата се
вижда, че при
съвпадение
на знаците на
остатъка и
делителя, в частното
се записва 1, тъй
като
делителят се
е съдържал в
нормализирания
частичен
остатък, а
следващата
операция е
изваждане.
Етапът
на
същинското
деление също
започва с
анализ на
знаците на
операндите, с
цел да се
определи
каква да бъде
първата
операция. В
този момент
делимото се
интерпретира
като остатък,
а така
определената
цифра -
като знак на
частното.
Логическата
функция,
която дава
стойност нa
поредната
цифра на
частното
според
таблица 3.2.8.1,
съответствува
на функция
логическа
равнозначност:
![]()
където
(n-1)-вите цифри
на частичния
остатък и на
делителя са
знаковите.
За
определяне
на
следващата
алгебрическа
операция,
преди
изместването
наляво, знаковата
цифра Rm[n-1] на
получената
разлика
трябва да се
запомни, тъй
като след
изместването
тя се губи.
Припомняме,
че за тази цел
в базовата
логическа
структура на
устройството
за деление от
фигура 3.2.6.3,
беше въведен
тригер ТВ.
Етапът
на
същинското
деление се
предхожда (за
числата с
дясно фиксирана
запетая) от
етапа на
лявата нормализация.
Когато се
нормализира
положително
число,
разпознаването
на
нормализирания
вид е твърде
елементарно - това
става по
наличието на
единица в
старшия (n-2)-ри
разряд
(напомняме на
читателя, че
непрекъснато
се
придържаме
към
определението
за структура
на
разрядната
мрежа, дадено
в тази книга на
фигура 1.1.6.1.3).
В
логическата
структура от фигура 3.2.6.3
за тази цел
се следи
изхода на
суматора - СМ[n-2]=?.
Когато
числата са
отрицателни,
стойността в
този бит обаче
не е
достатъчна,
ето защо е
необходимо
да се
синтезира
по-общ вид на
логическа
функция за
разпознаване
на
нормализиран
операнд в
допълнителен
код. Тази
задача е
значително
по-трудна, тъй
като
старшата
значеща
цифра на
отрицателното
число може да
бъде както
нула, така и
единица, а
освен това
отрицателните
числа имат и
едно
изключение -
числото Xmin.
Регулярният
случай на
нормализация
е свързан с
последователно
изместване
на операнда
наляво,
независимо
какъв е
знакът на числото,
докато
разпознаващата
функция
получи
стойност 1. За този
случай,
общият вид на
разпознаващата
функция може
да се приеме
за дизюнкция
от два
елемента:
![]()
съответно
разпознаващи
положителни
и отрицателни
числа.
Очевидно е,
че FN1
(функцията за
положителни
числа) ще има
вида:
![]()
Вторият
елемент FN2, който
трябва да
разпознава
нормализирани
отрицателни
числа,
определя
цифрата в (n-2)-рия разряд
като значеща,
с помощта на
всички
по-младши
разряди
взети заедно:
![]()
Признаците
EQ
и NEQ в горната
формула се
формират от
съдържанието
на
разрядната
мрежа в
интервала [n-3 ¸ 0]. Признакът EQ
приема
стойност
единица
когато в тази
част от
разрядната
мрежа има
само нули, а
признакът NEQ
приема
стойност
единица в
останалите
случаи.
За съжаление,
както беше
вече
отбелязано,
имаме и едно
изключение,
което следва
да разгледаме
отделно.
Наличието му
трябва да
бъде проверено
преди
регулярната
нормализация.
По същество
трябва да се
разпознае
двоичната
комбинация,
съставена от
една водеща
единица в (n-1)-вия
разряд,
следвана от (n-1) нули
комбинация,
която
представлява
допълнителния
код на
най-малкото
число: Xmin.
![]()
Ако
в разрядната
мрежа е
представено
това число,
то неговият
нормализиран
вид може да
се получи
след извършване
на аритметическо
изместване надясно
на един
разряд. В
зависимост
от това, дали
тази
стойност е стойност
на делимото
или на делителят,
отброяването
на това
изместване в БрЦ в
процеса на
нормализация,
трябва да
бъде с инверсен
знак, т.е.
обратен на съществуващото
действие в
регулярния
случай.
В
крайна
сметка
функцията за
разпознаване
на нормалния
вид на
числото ще
изразим така:
![]()
При
деление на
числа в
допълнителен
код съществува
опасност от препълване
дори в
случая,
когато операцията
е призната за
изпълнима по
силата на
неравенството
(3.2.6.1).
Препълването
възниква в
един
единствен
случай,
когато се
дели числото Xmin на
числото (-1). В този
случай
частното Xmin/(-1) е
положително
число и
надхвърля
възможностите
на
разрядната
мрежа, тъй
като модулът
на Xmin е
равен на
модула на
разрядната
мрежа S, за който се
знае че е
число
по-голямо от
числото Xmax (вижте
фигура 1.6.2.2).
От
гледна точка
на
алгоритъма
за деление, който
следва да се
синтезира,
това
препълване
може и следва
да се
разпознава.
То е различно
по смисъл от
ситуацията,
когато не е
изпълнено
условието за
дефинираност
на
операцията,
въпреки че и в
този случай
се
сигнализира
за препълване.
Препълването,
за което
говорим, може
да се
разпознае
още на етапа
на
нормализацията
в случай, че в
брояча БрЦ
се определи
брой на
неизвестните
цифри по-голям
от
максимално
възможния,
т.е. ако
![]()
Максимално
възможната
положителна
стойност в
брояча БрЦ е
равна на n.
Тази
стойност се
получава
когато
най-малкото
число Xmin
се дели на
числото (-1).
Тогава
според
описаната
нормализация
и според (3.2.6.5)
имаме N = (n-2) - (-1)+1 = n.
Посочената
по-горе
стойност
може да се
получи в
брояча на
циклите БрЦ
в още един
случай. Това
е случаят,
когато най-малкото
число Xmin се дели на (+1).
Ясно е, че
частното в
този случай е
равно на
делимото,
като този
резултат е
нормален и
той се
получава без
фактическо
деление, т.е.
прескача се
третия етап
от
алгоритъма.
След
завършване
на етапа на
същинското
деление в
допълнителен
код, така както
и при
операция
умножение, частното
не винаги е
вярно и
когато това е
така то се
нуждае от
корекция.
Корекцията
по същество
представлява
компенсиране
на недостига
в частното,
явяващ се
като
следствие от
това, че
операндите са
представени
с
изобразяващия
си код
(допълнителен
код).
Случаите на
необходимост
от корекция
са
представени
в таблица 3.2.8.2.
Таблица 3.2.8.2
Определяне
на
корекцията
|
Знак на
делимото X |
Знак на
делителя Y |
Стойност
на
корекцията |
|
+ |
+ |
няма
корекция |
|
+ |
- |
+1 |
|
- |
+ |
+1,
ако Rk-l+1 ¹ 0 |
|
- |
- |
+1,
ако Rk-l+1 =
0 |
В
заключение
може да
обобщим, че
алгоритъмът
за деление на
числа
представени
в допълнителен
код, може да
бъде
реализиран в
базовата
логическа
структура от фигура 3.2.6.3
след
незначителни
изменения,
които се отнасят
до следното:
1. Тъй
като
частното се
получава
автоматично
в
допълнителен
код,
началното
установяване
на регистъра
на частното РгZ
зависи от
знаците на
операндите.
Ако те са еднакви,
то РгZ:=0,
а ако са
различни: РгZ:=111...11.
Това изисква
управляващият
сигнал УС14 да бъде
поставен в
зависимост
от логическата
равнозначност
на знаците на
операндите.
Това
означава, че
за това
установяване
трябва да
въведем още
един
управляващ
сигнал, който
ще
установява в
този
регистър единици
и който ще
означим УС14а.
Установяване
на началното
състояние в РгZ
следователно
се извършва
след
приемане в устройството
на
операндите и
след анализ на
техните
знаци, както
е описано в
представената
по-долу
микропрограма.
2.
Условието за
изпълнимост
на
операцията се
разпознава
по това, че
знакът на
разликата (X-Y) не
съвпада със
знака на
делителя.
Това изисква
сравнение на
знаците, т.е.
прилагане
върху тях на
логическата
функция
неравнозначност.
3.
Необходима е
реализация
на
логическите
схеми на
функцията за
текущата
цифра в частното
zm според
(3.2.8.1), и на
функцията (3.2.8.5)
за
разпознаване
на
нормализиран
операнд,
представен в
допълнителен
код.
Логическите
функции FN1 , FN2 , FN3 следва
да се
реализират
върху
изходите на суматора,
което ще
означава, че
за да се формират
техните
истинни
логически
стойности за
съответния
операнд,
същият
трябва да
излезе на
изхода на суматора
непроменен.
4. В
случай че
бъде
разпознат
операнд,
равен на
най-малкото
число, т.е.
когато за
него възниква
признакът
(флагът) FN3=1, то тогава
съответният
операнд следва
да се измести
аритметически
надясно на 1
бит. За да
може да се
направи това
изместване
изходът на
суматора СМ следва да се
свърже
допълнително
още с входа
на РгСМ чрез дясна
коса връзка,
която да се
управлява от
допълнителен
управляващ
сигнал УС34
:
РгСМ:=АИД(СМ),
както е
показано на
следващата
рисунка:
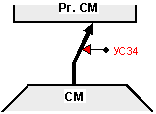
5. За
да се
разпознава
случаят на
препълване (3.2.8.6),
върху брояча БрЦ,
в който при
лявата
нормализация
се формира
броя на
неизвестните
цифри на
частното, следва
да се
реализира
допълнителен
изход от
дешифратора,
освен изхода
на признака
за съдържание
нула EQ. Можем
да означим
този признак
така Vn, Vn:(БрЦ)>(n-1).
Вече
пояснихме, че
в този случай
в брояча се
образува
числото n. Това
означава, че
в същност
съответствието
на признака Vn
е: Vn:(БрЦ)=n.
В
този общ
случай
получаваната
в брояча БрЦ
стойност
може още да
бъде както
равна на нула,
така и
по-малка от
нула, т.е.
отрицателна.
Ето защо се
налага още
един признак,
който ще
означим Pn, чието
съответствие
ще бъде: Pn : (БрЦ)<0.
6. Тригерът
на знака ТS в
разглеждания
алгоритъм ще
има предназначение
да запомни
първоначалната
стойност на
знака на
делимото,
който е
необходим в
края на
делението за
определяне
на необходимостта
от корекция
на частното.
Поради тази
причина ще се
измени и
схемата на
входната му
логика.
7. За да
може в случай
на нужда да
се осъществи
корекцията
на частното с
(+1), е
необходима допълнителна
връзка на
регистъра на
частното РгZ. При това
ще се окаже
удобно
крайният
резултат
(частното) да
се запише в
регистъра на
суматора РгСМ.
За да се
оеднаквят
двата
възможни
случая по
отношение
знака на
частното,
може да приемем,
че
регистърът
на суматора РгСМ
съдържа
резултата
във всички
случаи. Това налага
прехвърляне
на
съдържанието
на РгZ в РгХ,
откъдето с
или без
корекция
окончателният
резултат ще се
записва в РгСМ, който
ще се приема
за изходен
регистър на устройството
за деление. В
такъв случай
няма да бъде
необходима
изходната
връзка от регистър
РгZ към
шината за
данни.
8.
Предназначението
на тригера ТВ ще бъде
съхранено. В
него на всеки
такт ще се запомня
знаковата
цифра на
получения
частичен
остатък, с
чиято помощ
ще бъде
определяна
както
поредната
цифра в
частното,
така и следващата
операция.
9. Необходимо
е върху
съдържанието
на БрЦ да се
реализира
разпознаване
на всички
комбинации,
характеризиращи
случаите на
препълване
или предварително
известни
резултати.
10. Поредната
забележка,
която следва
да отбележим,
се отнася до
откриването
и реализацията
на корекцията
на частното
според
правилата,
изразени
по-горе чрез
таблица 3.2.8.2.
Необходимостта
от корекция +1
на текущата
стойност на
частното
може да се
определи с
помощта на
логическа
функция,
която може да
се синтезира
от таблица 3.2.8.2,
като нейните
аргументи са:
·
Знакът
на делимото,
който се
съхранява в тригер
TS ;
·
Знакът
на делителя,
който се
съхранява в
тригер РгДт[n-1] ;
·
И
признакът Zero,
който се
формира от СФПр, за текущия
частичен
остатък,
намиращ се в този
момент на
изхода на
суматора.
11.
Последната
забележка се
отнася до
особените
резултати Z=+1 или Z=-1. При
равенство на
операндите
частното е единица
със
съответен
знак.
Резултатът Z=+1 се
постига
директно в
изходния
регистър чрез управляващия
сигнал УС16b, а Z=-1 - чрез УС16а.
Всичко
изброено и
коментирано
по-горе ни довежда
до
логическата
структура,
представена
на
следващата
фигура 3.2.8.1. Структурата
е получена
въз основа на
базовата
логическа
структура за
деление в прав
код.
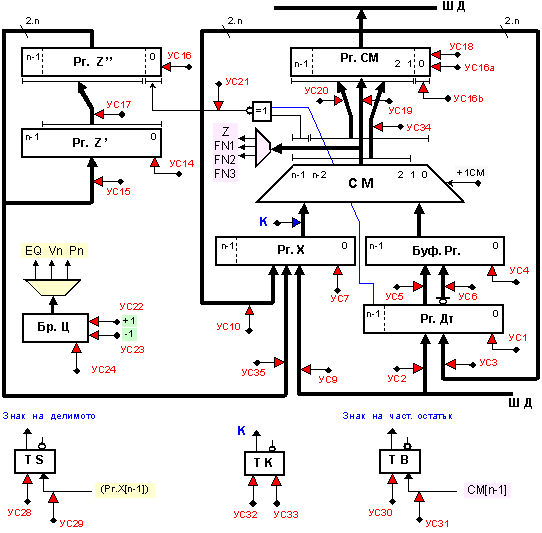
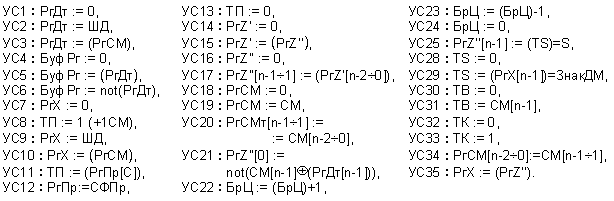
Фиг. 3.2.8.1.
Логическа
структура на
устройство
за деление на
числа
представени
в
допълнителен
код без възстановяване
на частичния
остатък по схемата
с неподвижен
делител
Окончателно
представяме
алгоритъма
за деление в
допълнителен
код,
изпълняван в
устройството,
представено
по-горе.
0:: начало // микропрограма
за деление в
допълнителен
код по метода
без
възстановяване
на остатъка
по схемата с
неподвижен
делител //
//---------
начално
установяване ------------//
1:: УС1 :
РгДт:=0 ,
УС4 : БуфРг:=0 , УС7 :
РгX:=0 ,
УС14 : РгZ:=0 , УС16 : РгZ:=0
,
УС18 : РгСМ:=0 , УС24 :
БрЦ:=0 ,
УС28 : TS:=0 , УС30 : TB:=0 , УС32 :
ТК:=0 ,
УС13 :
ТП:=0 ;
2:: УС9 :
РгX:=Дм ;
3:: УС2 :
РгДт:=Дт , УС29 : TS:=(РгX[n-1]) ; //
запомняме
знака на
делимото //
4:: УС31 :
ТВ:=(РгДт[n-1]) ; //
запомняме
знака на
делителя //
5:: УС5 :
БуфРг:=(РгДт) ; // на
изхода на
суматора
излиза
делителят //
//-------------
проверка на
условието за
дефинираност
Дт = 0 ? --------------//
6:: Ако Zero
то { V:=1 ; // прекъсване при деление на нула // премини
към 27:: } ;
7:: УС4 :
БуфРг:=0 , УС33 : ТК:=1 (К=1) ;
//--------
проверка на
условието за
изпълнимост
на
операцията ------------//
8:: УС6 :
БуфРг:=not(РгДт) , УС8 : ТП:=1
(+1СМ) ; // СМ=ДмДт //
// ако
знаците на
разликата и
на Дт
са различни,
условието за
изпълнимост
не е
изпълнено,
само ако
разликата на
изхода на
суматора не е
равна на нула //
9:: Ако ((СМ[n-1] xor (РгДт[n-1])) and (not Zero)) то { премини
към 27:: } ;
// край, Z=0. //
//--- образуваме
разликата за
да проверим
дали не са
равни модулите,
т.е. |Дм|-|Дт|=0? -----//
//-------- това е
проверка за
резултат Z=+1
или Z=-1
------------//
10:: УС4 :
БуфРг:=0 , УС13 :
ТП:=0 ;
11:: Ако ((TS) xor (РгДт[n-1])) то { УС5 :
БуфРг:=(РгДт) ;
премини
към 12:: ;
}
иначе { УС6 :
БуфРг:=not(РгДт) , УС8 : ТП:=1
(+1СМ) ; } ;
12:: Ако Zero
то //
резултатът е
единица със
съответния
знак //
{ Ако ((TS) xor (РгДт[n-1])) то { УС16b : РгСМ[0]:=1 ;
премини
към 27:: } ; // Z=+1 //
иначе { УС16а
: РгСМ:=111
11 ;
премини към 27:: } } ; // Z=-1 //
иначе { Ако (TS) xor (РгДт[n-1]) то // начална
стойност за
частното //
{ УС14а :
РгZ:=111...11 } } ;
//--------------------------- нормализация
на делителя ----------------------------//
13:: УС32 :
ТК:=0 (К=0) , УС4 :
БуфРг:=0 , УС13 :
ТП:=0 ;
14:: УС5 :
БуфРг:=(РгДт) ;
//--------
проверка за
изключителното
число Xmin ----------//
15:: Ако FN3 то { УС34 :
РгСМ[n-2¸0]:=СМ[n-1¸1] ,
РгСМ[n-1]:=СМ[n-1] ,
УС23 :
БрЦ:=(БрЦ)-1 ;
УС3 :
РгДт:=(РгСМ) , УС4 :
БуфРг:=0
;
премини
към 17:: ;
} ;
16:: Ако not(FN1 or FN2) то { УС20 : РгСМ[n-1¸1]:=СМ[n-2¸0] , РгСМ[0]:=0 ,
УС22 :
БрЦ:=(БрЦ)+1 ;
УС3 : РгДт:=(РгСМ) , УС4 :
БуфРг:=0 ;
УС18 : РгСМ:=0 , УС5 :
БуфРг:=(РгДт) ;
премини
към 16:: ; } ;
//---------------------------
нормализация
на делимото -------------------------------//
17:: УС18 :
РгСМ:=0 ,
УС4 : БуфРг:=0 , УС33 : ТК:=1 (К=1) ;
//--------
проверка за
изключителното
число Xmin ----------//
18:: Ако FN3 то { УС34 :
РгСМ[n-2¸0]:=СМ[n-1¸1] , РгСМ[n-1]:=СМ[n-1] ,
УС22 :
БрЦ:=(БрЦ)+1 ;
УС10 :
РгХ:=(РгСМ) ;
Ако Vn то {
Ако (TS) xor (РгДт[n-1]) то { УС4 :
БуфРг:=0 , УС33 : ТК:=1 (К=1) ;
УС19 :
РгСМ:=СМ
;
премини
към 27:: } ; // Z=Xmin, край //
иначе { V=1 ; премини
към 27:: } ;
// препълване //
} ;
} ;
//--------
проверка за
типичния
случай ----------//
19:: Ако not(FN1 or FN2) то { УС20 :
РгСМ[n-1¸1]:=СМ[n-2¸0] ,
РгСМ[0]:=0 ,
УС23
: БрЦ:=(БрЦ)-1 ;
УС10 :
РгХ:=(РгСМ) ;
УС18 : РгСМ:=0 ;
премини
към 19:: ; } ;
//--------
край на
нормализацията ----------//
20:: Ако (EQ or Pn) то { премини
към 24:: } // Z=0,
тъй
като (БрЦ)=0 или (БрЦ)<0 ;
край //
//----------------------------- начало
на
същинското
деление -----------------------//
21:: Ако ((TS) xor (РгДт[n-1])) то
{
събиране:
УС16 : РгZ:=0
,
УС18 : РгСМ:=0 ,
УС5 : БуфРг:=(РгДт) , УС13 : ТП:=0 ;
УС21 : РгZ"[0]:=Zm , //
поредната
цифра на Z //
УС31 : TB:=СМ[n-1] ,
УС17 :
РгZ"[n-1¸1]:=(РгZ'[n-2¸0]) ,
УС20 : РгСМ[n-1¸1]:=СМ[n-2¸0] , РгСМ[0]:=0 ,
УС23 :
БрЦ:=(БрЦ)-1 ; }
иначе { изваждане:
УС16 :
РгZ:=0 , УС18 :
РгСМ:=0 ,
УС6 : БуфРг:=not(РгДт) , УС8 :
ТП:=1, (+1СМ) ;
УС21 : РгZ"[0]:=Zm , //
поредната
цифра на Z //
УС31 : TB:=СМ[n-1] ,
УС17 : РгZ"[n-1¸1]:=(РгZ'[n-2¸0]) ,
УС20 : РгСМ[n-1¸1]:=СМ[n-2¸0] , РгСМ[0]:=0 ,
УС23
: БрЦ:=(БрЦ)-1 ; } ;
22:: УС15 :
РгZ':=(РгZ") ,
УС10 : РгХ:=(РгСМ) , УС4 :
БуфРг:=0
;
//---------------
проверка за
преждевременно
точно
деление ------------------//
23:: Ако Zero
то { премини
към 24:: } // ако
остатъкът е
равен на
нула //
//
преждевременно
точно
деление //
иначе
{ Ако EQ то {
премини
към 21::
} // ако (БрЦ)=0
//
иначе
премини
към 18:: } ;
24:: [
изпълнение
процедура "Корекция" ] ;
25:: Ако notEQ то {
УС16 : РгZ":=0 ;
УС17 :
РгZ"[n-11]:=(РгZ'[n-20]) , УС23 :
БрЦ:=(БрЦ)-1 ;
УС15 :
РгZ':=(РгZ") ;
иначе { премини
към 27:: } } ;
26:: премини
към 25:: ;
//
добавяне на
младшите
незначещи нули //
27:: край ;
//----------------------------- начало
на
процедурата
Корекция -------------------------//
( процедура "Корекция"
)
//----------------------------- край на
процедурата
Корекция ----------------------------//
Синтезът
на част от
логическите
функции, както
и на
възможното
оптимизиране
на логическата
структура и
на
микропрограмата
на
алгоритъма
за деление в
допълнителен
код, оставяме
на любознателния
читател.
Негово дело
следва да бъде
още
записването
и добавянето
на процедурата
Корекция
към горната
микропрограма.
Ще
добавим, че
написаното в
раздел 3.2.6
относно
определянето
на остатъка
като цяло
число и като
втория
резултат
освен
частното, е в
сила и при
представения
по-горе
алгоритъм.
Числени
примери
читателят ще
намери в книга
[2].
Следващият
раздел е:
3.2.9 Методи
за
ускоряване
на операция
деление ( Methods to accelerate division )