3.3.3. Операция
деление на
числа с ПЗ
Division
Операция деление на числа, представени във форма с плаваща запетая, се изразява по следния начин:
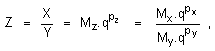
където q е
основата на
бройната
система, в
която са изобразени
числата.
По-надолу, при
представяне
на отделните
етапи на алгоритъма,
се има
предвид
двоична
бройна система.
След
извършване
на
математическите
преобразувания
изразът
добива вида:
![]()
От
горния запис
се вижда, че
частното Z
ще има
мантиса Mz, която ще
се получи в
резултат на
деление на
мантисите на
двата
операнда, а
порядъкът му pz ще се
получи като
разлика от
порядъците
на делимото и
делителя:
![]()
Става
ясно, че
операция
деление на
числа с плаваща
запетая се
осъществява
чрез познатите
вече
операции
деление и
изваждане на
числа с
фиксирана
запетая. Тези
две операции
са независими
и могат да се
изпълняват
паралелно
във времето.
Алгоритъмът
на тази операция
съдържа
следните
етапи:
1.
Проверка на
значенията
на мантисите.
Алгоритъмът
за деление на
числа с
плаваща
запетая не
може да подмине
необходимите
логически
проверки,
отнасящи се
до условието
за изпълнимост
и условието
за дефинираност
на
операцията.
Последното
изисква
проверка на
мантисата на
делителя. При
делител нула
операцията
завършва с
флаг за
препълване и
резултат +∞
или -∞.
Що
се отнася до
условието за
изпълнимост,
то се
изразява
чрез
неравенство,
обратно на (3.2.6.1),
предвид на
това, че
мантисата е
правилна дроб.
Като се
отчете обаче
способността
на разглежданата
форма за
представяне
на числата,
да променя
положението на
значещите
цифри спрямо
запетаята,
проверката
на това
условие
става ненужна.
Това се дължи
на факта, че
мантисите на
двата
операнда са с
ляво
фиксирана
запетая, при
това са
нормализирани.
Ето защо
мантисата на
частното
може да се
разглежда
като полином
винаги от
нулев ред,
чиито
коефициенти
се получават
последователно
от старшите
към младшите
в резултат на
m
на брой
последователни
прехода в
цикъла на
същинското
деление. С
други думи
етапът на
лявата
нормализация
в алгоритъма
тук липсва, а
броят на
неизвестните
цифри на
частното е
предварително
известен – те
са m на брой, т.е.
предварителната
стойност на мантисата
на частното
се търси във
вида:
![]()
В
случай, че
делимото е
числото нула,
за резултат
се приема
числото нула
и операцията
завършва.
2.
Същинско
деление.
Когато
обаче и двата
операнда са
различни от
нула,
мантисите
трябва да се
разделят фактически,
при което се
получава
споменатото
по-горе
m-разрядно
число. Това
число има цяла
част, която
може да бъде
различна от
нула, ето
защо следва
да оценим
възможния
диапазон за
стойността
на
отношението.
Модулът на
полученото
частно се
намира в
границите:
![]()
които
са получени
като се имат
предвид стойностите
на
минималната
и на максималната
нормализирана
мантиса в
разрядната
мрежа , както
бяха
определени в
предходния
раздел.
От
указаните
граници на (3.3.3.2)
става ясно,
че мантисата Mz мoже да се
получи като
нормализирана
или като
ненормализирана
отдясно, т.е.
предварителната
стойност на
мантисата на
частното
може да има един
от следните
два вида:
±0,1zzz…zz - вид
на лявата
граница;
±1,zzzz…zz - вид
на дясната
граница.
С други думи отношението на мантисите може да бъде нормализирано число или число с препълване. От казаното следва, че алгоритъмът за деление трябва да завършва с процедурата за нормализация на резултата. Ако такава е необходима, частното се измества на един разряд вдясно, а порядъкът се компенсира с прибавяне на една единица, при това следва да бъдат отчетени всички възможни случаи в полето на порядъка. Следва още да отбележим, че изместването на мантисата надясно причинява загуба на един младши бит, което е неизбежна грешка.
В реалния вътрешен формат на числата с плаваща запетая обаче в мантисите се явява скритият бит. Така техниката на скрития бит променя споменатите по-горе величини както следва – минималния модул на мантисата е
![]()
а
максималния
![]()
От тук модулът на възможното часно от мантисите се определя в следния диапазон. Отляво
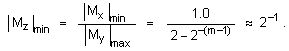
и
отдясно
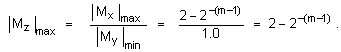
Така
интервалът
за
възможните
стойности на
часното
приема вида
![]()
което
означава, че
стойността
на мантисата Mz към този
момент може
да има
ненормализиран
вид, т.е.
предварителната
стойност на
мантисата на
часното може
да се намира
в интервала:
±0,1zzz …
zz - вид на
лявата
граница;
±1,zzz
... zz - вид
на дясната
граница.
И в този случай часното на мантисите може да бъде нормализирано число или число, което следва да се нормализира чрез изместване наляво на един бит. Заедно с това порядъкът (характеристиката) трябва да бъде коригиран чрез изваждане на една единица. При това в полето на характеристиката може да настъпи положително препълване.
Паралелно с делението на мантисите може да се извърши изваждане на порядъците. Тъй като порядъците са числа със знак това естествено се извършва в допълнителен код. Получената разлика е само предварителна стойност на порядъка на резултата. При получаване на тази разлика е възможно да настъпи препълване, което следва да се интерпретира във връзка с полученото частно.
3.
Нормализация
на резултата.
В
структурата
на
разрядната
мрежа без скрит
бит, когато
се налага
нормализация
на мантисата
на часното,
се извършва
изместване
на надясно
на един
разряд, тъй
като
полученото
часно е число
равно или
по-голямо от
единица. В
този случай е
необходима
компенсация
на порядъка.
Към
предварителната
стойност на
порядъка се прибавя
единица, при
което е
възможно да
настъпи положително
препълване
в полето на
порядъка.
Положителното
препълване е
само на един
порядък и е
възможно, ако
предварителната
стойност на
порядъка е
равна на pmax.
Предварителната,
т.е.
неокончателната
стойност на
частното в
този случай
може да се изрази
по следния
начин:
![]()
Това е
ситуация, при
която след
опит да се отстрани
препълването
в полето на
мантисата, е
възможно да
настъпи
препълване в
полето на
порядъка и
обратно. Тази
ситуация е непоправима,
в резултат на
което може да
се вземе решение
за
окончателно "препълване
при плаваща
запетая".
Описаните
две
препълвания
са взаимно
свързани и не
могат да се
преодолеят.
Единственият
шанс този
резултат да
се запази
като нормален
и да участва
в следващите
изчисления е
той да се
приеме в този
си вид, което
е възможно
само в
разрядна
мрежа,
използваща техниката
на скрития
бит (фигура
1.1.6.2.4).
Този факт е
една
допълнителна
обосновка за
прилагането
на тази
техника в
стандарта на
IEEE (вижте пункт
1.1.6.2).
Освен
това
предварителната
стойност на порядъка
на частното
може да бъде
получена с
дълбоко
положително
препълване,
достигащо до 2.pmax,
което в
описвания
случай на
мантисата,
налагаща
компенсацията
+1, само ще бъде
допълнително
засилено.
Естествено в
този случай се
взема
решение за
окончателно "препълване
при плаваща
запетая".
При
изваждането
на порядъка
на делителя от
порядъка на
делимото
може да
настъпи още и
отрицателно
препълване.
В зависимост
от степента
на този вид
препълване
също могат да
се разгледат
различни ситуации.
За първа
ситуация
можем да
допуснем
отрицателно
препълване в
полето на
порядъка
само с една
единица. Това
е случай,
когато
реалната
стойност на разликата
от
порядъците е
числото (pmin–1).
Веднага може
да се
съобрази, че
това препълване
може да бъде
отнето при
нормализация
на мантисата,
ако такава се
налага. Ако
обаче
отрицателното
препълване е
достатъчно
дълбоко,
достигащо
дори до 2.pmin,
то не може да
бъде отнето.
Ясно е, че в
такива случаи
за резултат
следва да се
приеме числото
нула (машинна
нула).
Ако
обаче
отрицателното
препълване
не е
по-дълбоко от
(m-2) единици и
ако има
възможност
за работа в
режим на недостиг,
вместо
приемане на
резултат
числото нула,
мантисата
може да се
измести още
няколко
разряда
надясно, до
достигане на
минимално
представимата
за порядъка
стойност.
Както и при
операция
умножение, в
режим на
недостиг,
порядъкът не
може да бъде
друг освен pmin, тъй като
само при тази
стойност
мантисата може
да
съществува с
максимален
брой значещи
цифри.
Подобен
резултат би
имал общия вид
(3.3.2.5). Крайните
резултати,
които тук
могат да се
приемат след
изваждането
на
порядъците,
както и при
операция
умножение,
също дават
основания за
известна преднина
(преднина в
реда oт
микрооперации)
на операцията
върху
порядъците
пред
операцията върху
на мантисите.
Когато
разрядната
мрежа
изполва
техниката на
скрития бит,
тогава, както
беше
посочено
по-горе ненормалността
на мантисата
на часното се
отстранява
чрез
изместване
на един бит наляво.
Компенсацията
на порядъка
(характеристиката)
е свързана с
ефекти, които
са аналогични
с вече
описаните и
по тази
причина няма
да
утежняваме
изложението.
Същинското деление на мантисите започва с определяне на цифрата в цялата част на частното, а възможните за приложение алгоритми за деление на мантисите бяха вече разгледани. Делението може да бъде точно или с остатък.
Забележка. Всичко
казано до
момента се
изпълнява
при условие,
че частното
се дефинира в
интервала (3.3.3.2).
Съществува
обаче
вероятност операндите
да имат
мантиси,
които са
получени
като
резултати от
предидущи
операции в условията
на недостиг,
т.е.
мантисите на
операндите
могат да не
са
нормализирани.
Това означава,
че е възможно
частното от
такива мантиси
да бъде силно
денормализирано,
при това в
двете
направления. Тази
възможност
не е
разгледана в
регулярния
случай, ето защо
реалният
алгоритъм се
усложнява
допълнително
и ако
читателят
желае може да
изследва
това негово
разклонение,
което няма да
представлява
съществено
затруднение,
тъй като
всички
основни и
възможни
ситуации
бяха вече
изяснени.
Както
и
предидущите
операции,
така и
операция
деление се
интерпретира
много
относително
в светлината
на математическите
закони. Като
се има
предвид, че частното
има краен
брой цифри,
т.е. че то се подчинява
на функцията round - (3.3.1.14), за
деление на
числа
представени
във форма с
плаваща
запетая по
изказания
по-горе алгоритъм,
са в сила
следните
тъждества:
FLOAT(a/b) = round(a/b, v) ;
(3.3.3.4)
FLOAT [(-a)/b]
= FLOAT [a/(-b)] = -FLOAT(a/b) ; (3.3.3.5)
FLOAT(0/a) = 0ПЗ ; (3.3.3.6)
FLOAT(a/1) = аПЗ ; (3.3.3.7)
FLOAT(a/a) = 1ПЗ ; (3.3.3.8)
Ако ( а
≤ b and c > 0 )
,
то FLOAT(a/c) ≤ FLOAT(b/c)
;
и FLOAT(c/a) ≥
FLOAT(c/b) ; (3.3.3.9)
Илюстрацията
на
алгоритъма
за деление на
числа
представени
във форма с
плаваща запетая
както без,
така и с техниката
на скрит бит,
е изложена
подробно с
множество
числени примери
в книга
[2].
Следващият
раздел е:
3.3.3.1.
Необходима
ли е
нормализация
за числата с
плаваща
запетая? ( Is normalization necessary for loating point numbers? )