ГЛАВА
4
Операционни схеми
Operating
logical schemes
|
4.5. Оценка на производителността при конвейерна организация на
изчисленията |
|
4.9. Асинхронен модел на фактическото
закъснение за цифров компаратор |
В раздел 2.1 представихме нашето разбиране относно
възможността за реорганизация на линейни алгоритмични структури, което може да
бъде постигнато само чрез обединяване на операционните логически схеми. В тази
връзка искаме да подчертаем изключителното значение на аритметическата операция
събиране, като първична операция и като операция с една от най-големите
латентности, оказваща влияние на всички останали аритметични операции. В
преследване на възможно най-високата производителност, заедно с всички останали
подходи, от изключително значение е икономията на латентност при изпълнение на
всяка отделна микрооперация. Ето защо е актуална задачата за създаване в
операционните схеми на възможност за ефективна работа в условията на реално
асинхронно управление. Хардуерната реализацията на модела на фактическото
закъснение CD (Copmlete Detection)
е свързана със значителни апаратни разходи, ето защо е добре дошла всяка идея,
способстваща тяхното минимизиране. В тази глава са разгледани различни подходи
за синтез и реализация на модела на фактическото закъснение. Разгледани са още
задачите за събиране на два, три и повече операнда едновременно. Представено е
едно приложение на концентратор (суматор на три числа) при построяването на
конвейерен схемен умножител.
4.1.
Асинхронен двоичен комбинационен суматор
Операция събиране на числа, представени в
двоична бройна система е основна и неизбежна операция при техническата
реализация на изчислителен процес. Тази операция е първична и на нея се
основават всички други аритметически операции, ето защо вниманието към нея е
постоянно и неотклонимо. Предложени са множество подходи за синтез на този
логически възел (вижте книга
[2]). Всички те
целят единствено повишаване на бързодействието на суматора чрез минимизиране на
времето му за превключване. Тук обаче ние няма да се интересуваме от логическия
синтез на самия суматор, а само от синтеза на схема, чрез която във всяка
негова разновидност ще може да бъде вграден модела на фактическото закъснение. Този модел ще
отстрани непроизводителните времеви интервали при всяко събиране в условията на
асинхронно управление. Ние няма да изследваме
възможните структурни решения за логическата схема на суматора. Ще покажем само
възможността за създаване на условия за пълноценната му реализация като
логическа схема в структурата на асинхронно микроконвейерно звено, което
означава реализация според модела на фактическото закъснение. Тук тези възможности са показани при синтеза на многоразряден двоичен комбинационен суматор с
ускорен последователен пренос.
4.1.1.
Постановка на задачата
Оценката на максималното време за
превключване на един суматор позволява да се определи максималната честота, с
която той може да се извършва операция събиране при синхронно управление.
Смисълът на последното се състои в това, че към всяко следващо събиране може да
се пристъпва след изчакване на максималното време за превключване на n-разрядната му логическа схема.
Максималното време за превключване е реално
време за превключване само за определени операнди, предизвикващи възможно
най-дългата верига за разпространение на преноса. Такива операнди се срещат
рядко, което означава, че в повечето от случаите, сумата ще бъде готова
значително по-рано във времето. Анализът на тази ситуация води до идеята за
синтез на суматор, позволяващ прилагане в структури с асинхронно управление,
което води до значително по-висока производителност. Производителността се
повишава благодарение на това, че се натрупва спестеното време от всяка отделна
операция, за което могат да бъдат изпълнени допълнителен брой операции.
Така в сравнението между двата метода за
управление на изчислителния процес печели асинхронното управление. Печалбата
расте с нарастване на броя на изпълнените операции. Стремежът към това
положително качество актуализира задачата за синтез на асинхронен суматор или
суматор по модела Copmlete Detection.
Наименованието асинхронен суматор също се
нуждае от пояснение. Ще разбираме всеки суматор като асинхронен, ако той може
да работи в условията на асинхронно управление. За целта той трябва да е
способен сам да обявява края на своето превключване след събиране на всеки два
нови операнда.
4.1.2.
Синтез на асинхронен суматор с ускорен последователен пренос
Тук ще представим синтеза на асинхронен
суматор с ускорен последователен пренос и ще дадем оценка на получената схема.
Това не означава, че концепцията и получените резултати не могат да се приложат
върху суматори с друга структура, например с паралелен пренос, с групов пренос
и пр. Суматорът е именуван с ускорен последователен пренос, тъй като редува
фазите на функцията на преноса (права и инверсна) и въпреки че остава с
последователен пренос, има двойно по-малко време за превключване в сравнение с
класическия суматор.
Хардуерната реализация на операция събиране,
която изразяваме така z=x+y,
където с x и y са означени двата
операнда (двете събираеми), а със z получената сума, в условията на асинхронно управление изисква
изработването на логически сигнал, който да маркира момента на поява на
истинната сума. Такъв сигнал може да бъде използван като сигнал за фиксиране на
резултата, а така също и като сигнал за начало на ново (следващо) събиране. С
други думи, за да бъде фиксиран резултатът, някой трябва да съобщи, че той е готов.
Синтезът на този сигнал търсим в смисъла на
следното твърдение: събирането на операндите е завършило, ако то е завършило в
първия, във втория и в последния разряд. С други думи, сигналът "край на
събирането" (СD, Complete
Detection) е една конюнкция от поразрядните сигнали за край на
събирането, а указаният момент ще се маркира от неговия положителен фронт.
![]()
По аналогичен начин може да се определи и
поразрядният сигнал за край на събирането, като неговият положителен фронт се
търси чрез дизюнкцията на възникващия в разряда пренос pi, т.е.
![]()
Предложеният израз (4.1.2), според алгебрата
на логиката, е константа - логическа единица във всеки един момент от
времето:
![]()
Тук обаче синтезът на функцията CDi
се основава на практическото несъвършенство на електронните схеми, реализиращи
логическите стойности, според които логическите стойности възникват в течение
на времето, а не мигновено. С други думи, полезността на горната дизюнкция се
изразява в нейното несъвършенство. За да бъде обаче то оползотворено в смисъла
на функцията, която целим, фронтовете на превключване на двете фази на всеки
отделен пренос, трябва да се явяват паралелно във времето. Тогава дизюнкцията
(4.1.2) ще съдържа практически "дефекти", като показаните на фигура
4.1.1.
![]()
Фиг. 4.1.1. Практическо
смущение в константата (4.1.2)
За надеждно оползотворяване на смущенията,
които в същност са израз на протичащия във времето процес, от чието начало и
край се интересуваме, е необходимо да формираме от показаните смущения
правоъгълен нулев импулс. Такива средства съществуват и те са представени
изчерпателно в глава 5, раздел 5.1.
След формиране от тези смущения на
краткотрайна нула, става възможно реализирането на функцията (4.1.1), като
конюнкция от последователни във времето логически нули. За да бъде отчетено
реалното време за превключване на логическите елементи, които изчисляват
стойността на преноса, поразрядните сигнали за край на събирането CDi
трябва да се формират от паралелно
изчислените във времето логически стойности на функциите pi и
not(pi). Паралелността може да се постигне само ако тези
функции се изразят като функции от едни и същи аргументи, а не една от друга.
За целта в схемата на суматора с ускорен последователен пренос следва да се
добавят липсващите логически функции. Както казахме в началото, суматорът с
ускорен последователен пренос редува фазите на функцията на преноса. В
разрядите с четни номера, където е реализирана правата фаза на функцията p2i,
трябва да се добави функцията на нейната инверсна фаза
![]()
а в нечетните разряди – функцията на нейната права фаза
![]()
Окончателният вид на сигнала "Край на
събирането" ще изразим така
![]()
където с буква F сме изразили
функцията за формиране на правоъгълен нулев импулс от фронтовото смущение в
дизюнкцията
![]()
На фигура 4.1.2 са представени младшите 3
разряда от принципната логическа схема на асинхронен двоичен комбинационен
суматор с ускорен последователен пренос.
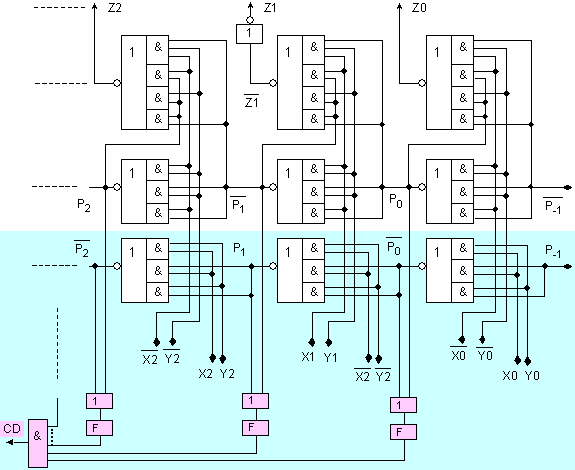
Фиг. 4.1.2. Принципна
логическа схема на асинхронен суматор
Елементите в схемата, означени с буква F, по
същество удължават във времето появяващата се логическа нула на изхода на всяка
схема ИЛИ, като отместват във времето предния фронт на генерираната нула.
Следва да се разбира, че когато има нова стойност на преноса в даден разряд,
това означава че има превключване, от чието начало и край се интересуваме.
Последователният пренос означава конкатенация във времето на сигналите CDi,
което не гарантира надеждно изчисление на конюнкцията (4.1.1). За да осигурим
тази надеждност трябва да осигурим застъпване във времето на последователно
следващите нули на сигналите CDi. Само така може да се
гарантира активната логическа нула на сигнала СD върху изхода на схемата И. Процесът на това формиране в три
последователни разряда е показан на времедиаграмата от фигура 4.1.3, където е
изобразено как след появата на нови данни на входа на суматора (т.е. моментът,
който приемаме за стартиране на операцията), се разпространяват преносите и се
формират поразрядните сигнали CDi, и още как се формира
тяхното разширение и крайният резултат - изходният за цялата схема сигнал СD.
Подобно последователно разпространение на три преноса настъпва например при
събиране на числата 7 и 1 (7+1=8). Продължителността на сигналите CDi е един фронт, а тя е означена с t [s].
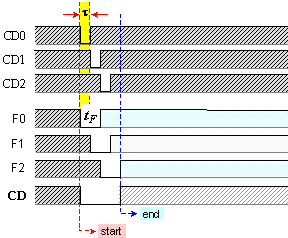
Фиг. 4.1.3. Начало
и край на събирането
Надеждното застъпване във времето на логическите
нули от изходите на елементите F изисква разширението им отдясно с дължината
поне на още един фронт, така че да бъде изпълнено отношението
![]()
Именно при това отношение е построена
времедиаграмата на фигура 4.1.3.
От фигура 4.1.2 може да получим оценката за
апаратните разходи при реализиране на n-разряден суматор, а от фигура 4.1.3 оценката на времето за
превключване на схемата. Последната е абсолютна или още фактическа
и се отнася за събиране на два конкретни операнда. Фактическото време за
събиране на два конкретни операнда се определя от онази верижка от
последователни преноси, която има най-голяма дължина. Както вече беше
споменато, оценката за повишеното бързодействие следва да се получи в резултат
на статистическо наблюдение на изпълнението на предварително определен брой
събирания. За да бъде оценката обективна операндите при тези събирания следва
да бъдат генерирани като случайни числа с равномерен закон на разпределение.
Очевидният извод, който може да се направи е, че за възможността да събираме в
режим на асинхронно управление, като отчитаме фактическата продължителност на
операцията, сме заплатили с нарастване на апаратните разходи. Допълнителните
апаратни разходи са изобразени в синята зона на схемата от фигура 4.1.2 и както
може да се съобрази, нарастването е с повече от 50%. В същото време суматорът е
останал с последователен пренос и повишеното бързодействие не е абсолютно
гарантирано, а има статистически смисъл.
4.1.3.
Минимизиране на апаратните разходи
Увеличените с повече от 50% апаратни разходи
за реализация на логическата схема на суматора е твърде висока цена за
допълнителния изход CD. Като имаме предвид броя на суматорите в една
реална схема, това решение е твърде скъпо, ето защо става актуална задачата за
минимизиране на апаратните разходи.
Представеното по-горе решение може да се характеризира с
пределните си изисквания по отношение на паралелността, която беше наложена
върху фронтовете на двете фази на функцията на преноса. Това беше и източникът
на допълнителните апаратни разходи. Това изискване може лесно да бъде снето,
ако във всеки отделен разряд стойността на липсващата фаза на преноса бъде
получавана от наличната, чрез логическо инвертиране., т.е. ще бъде изчислявана
последователно. Веднага става ясно обаче, че при такова схемно решение,
фронтовете на двете фази няма да причиняват смущенията, илюстрирани на фигура
4.1.1, тъй като дизюнкциите (4.1.2) ще станат почти идеални. За да осигурим
решението, ще използваме симетрични закъснителни линии DL, които са пояснени в
раздел 5.1.
За да постигнем надеждно описания ефект в
последователната дизюнкция (4.1.2), следва да засилим условието на разширението
до следния вид
![]()
В резултат на казаното, логическата схема,
която ще реализира поразрядния сигнал CDi, ще има вида,
показан на фигура 4.1.4.
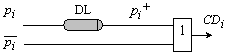
Фиг. 4.1.4. Логическа
схема за реализация на разширения поразряден сигнал
Превключването на логическите елементи от
предложената схема е представено на фигура 4.1.5.
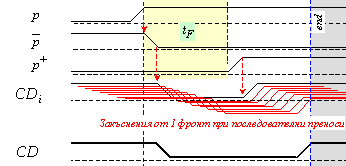
Фиг. 4.1.5. Времедиаграма
за формиране на сигнала СD
Вижда се, че активната стойност (нула) на
тази функция се формира от застъпващите се във времето и последователно
разпространяващи се сигнали. Предният (положителният) фронт на сигнала СD
отбелязва момента за край на операцията. Следващото събиране може да бъде
стартирано веднага след запис на получената сума, т.е. някъде в сивата зона на
рисунката.
Последното съображение, което трябва да
изкажем, се отнася до това, че схемата от фигура 4.1.4, следва да бъде
съобразявана в какъв пореден разряд ще бъде поставяна. Когато тя се поставя в
разряд с четен номер (0, 2, 4, ...), закъснителният елемент DL, следва да е
включен във веригата на правата фаза на преноса, а когато тя се поставя в разряд
с нечетен номер (1, 3, 5, ...), закъснителният елемент DL, следва да е включен
във веригата на инверсната фаза на преноса.
В резултат на изложеното, принципната
логическа схема на асинхронния суматор се променя и приема вида от фигура
4.1.6.
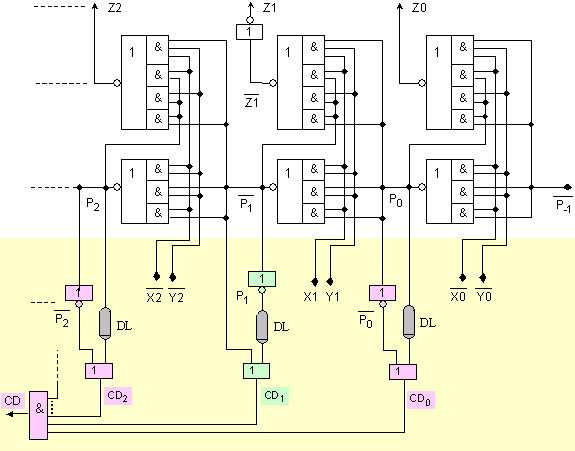
Фиг. 4.1.6. Принципна
логическа схема на асинхронен суматор (облекчена реализация)
Вижда се, че от първоначалния вариант на
схемата е премахната паралелната верига от логически елементи, изчисляващи
противоположната фаза на получаваните преноси. Вместо нея са въведени
симетричните закъснения DL. Тъй като в суматора с ускорен последователен пренос
фазите на преносите се редуват, то и схемите за реализация на функциите CDi
са различни и също се редуват.
Заключение
Синтезираните логически схеми реализират основната
аритметическа операция така, щото тя може да се изпълнява с възможно най-висока
степен на повторяемост. Времето за изпълнение на операцията се оценява
фактически от оригинална логическа схема на сигнала “Край на събирането”, който
в същото време може да се използва като сигнал в асинхронно управлявани
структури. Логическата схема на сигнала СD е представена в два варианта.
Тези логически схеми могат да бъдат използвани за оценка на фактическата
латентност практически за различни по вид суматори, умножители, делители и
други операционни схеми.
4.2.
Едновременно събиране на повече от 2 числа
Прилагайки нашето разбиране от раздел 2.1 за обединяване
на операциите, тук ще разгледаме резултатите върху операция събиране.
4.2.1. Постановка на задачата
Операция аритметическо събиране е
двуместна операция, т.е. в нея участват два операнда. От техническа гледна
точка обаче нищо не пречи да поставим въпроса за едновременно събиране на
повече от два операнда, което е резонно, като имаме предвид математическите
изрази с много операции.
Ще разгледаме случай на събиране на 3
числа, т.е. z=x1+x2+x3. Изчислението на тази сума изисква изпълнението на 2
последователни операции събиране чрез два 2-входови суматора. Така изказаната
представа ни води до следната последователна логическа структура
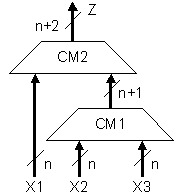
Фиг. 4.2.1. Логическа структура с 2-входови суматори
Тази постановка на задачата е известна от
литературата за еднобитови суматори. Последните са известни под наименованието
концентратори. Пълноразрядното
решение, което търсим тук, ни е необходимо като градивен елемент за следващи
постановки.
Анализът на схемата изявява разрядно
разширение в междинния и в окончателния резултат. Това разширение прави
суматорите различни. Ако суматор СМ1 е n-разряден, то суматор СМ2 трябва да е (n+1)-разряден.
В същност, най-старшият разряд на междинната сума ще се представлява от
най-старшия пренос в суматор СМ1. И въпреки, че Х1 е n-битово число, суматор СМ2 има един
пълен разряд в повече. Аналогично, разрядността (n+2) на крайната сума
се формира, включвайки като най-старша цифра най-старшия пренос от суматор СМ2.
Разрядността изисква съответно комутиране на входните даннови връзки към
разрядите на операндите.
4.2.2. Принципна схема
Върху логическата структура от фигура 4.2.1
ще приложим концепцията за обединяване на комбинационните схеми, представена в
раздел 2.1, въпреки очевидното удобство за конвейерна организация на това
събиране. За да получим принципната логическа схема на суматор за три операнда
ще разгледаме събирането им на ниво битове, както е показано на фигура 4.2.2.
Z = < bzn+1
bzn bzn-1 …
bz2 bz1 bz0 >.

Фиг. 4.2.2. Схема на поразрядно събиране
На фигурата с bx1, bx2, bx3 и т.н. са означени отделните
двоични цифри на числата x1, x2 и x3, а с Y и Z – междинната и крайната суми
съответно.
От схемата по-горе
се вижда, че междинната сума Y може да се получи като поразрядна без отчитане
на възникналите преноси при събирането на първите 3 цифри във всеки разряд.
Технически тази сума може да се получи с помощта на n на брой пълни едноразрядни двоични
суматори, наредени един до друг без всякаква връзка между тях. В същото време
възникналите от тези суматори преноси (съответно подредени като (n+1)-разрядно
число) трябва да се съберат с междинния резултат Y, за което е необходим пълен n-разряден
двоичен суматор, на чийто изход излизат окончателните стойности на разрядите в
крайната сума
Специално ще
отбележим, че най-младшият разряд в сумата е готов още след първото събиране.
Казаното води до следната схема от фигура 4.2.3.
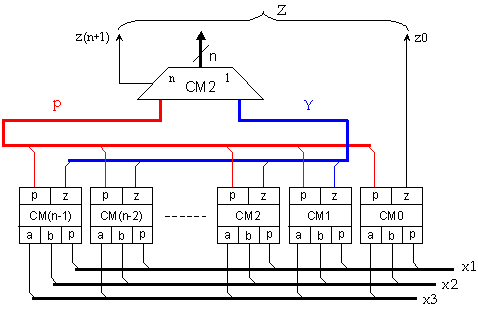
Фиг. 4.2.3. Схема на 3-операнден двоичен суматор
Не може да отречем, че и тази схема има структурното
удобство за конвейерна организация на събирането, но тук тя ще бъде оценена
като самостоятелен градивен елемент. Схемата е достатъчно близка до принципната
логическа и позволява да се определи максималното закъснение на резултата.
Вижда се, че всички цифри на междинната сума Y получават истинните си стойности
едновременно.
Като имаме предвид
принципната логическа схема на пълния едноразряден суматор (вижте книга [2]), закъснението на
Y е максимум (3.t) секунди.
Ще приемем, че
суматорът СМ2 е изпълнен по структурата с ускорен последователен пренос, която
е най-икономична. Такъв суматор ще добави закъснението (n+2).t. Следователно, окончателното време за превключване на
схемата от фигура 4.2.3, ще оценим както следва
![]()
където с t е означено времето за превключване на един
градивен логически елемент в схемата на суматора.
В същото време, изходната структура от фигура
4.2.1, за която казахме, че е удобна за конвейерна организация, може да оценим
като такава по следния начин. Суматорите, от които тя се състои, могат да бъдат
реализирани по различна структура, но за типичния избор, който сме направили и
в предходния раздел, ще приемем, че те са с ускорен последователен пренос.
Оценката на времето за превключване на такъв n-разряден суматор (при n четно) е следната
![]()
Оценката на времето за превключване на (n+1)-разряден
суматори е следната
![]()
Оценката е същата, защото числото (n+1)
е нечетно.
Така оценката на времето за превключване на
структурата от фигура 4.2.1 като конвейерна, т.е. като последователна, ще бъде
следната
![]()
Образувайки, с цел сравнение, отношението
между оценките (4.2.1) и (4.2.4), получаваме резултата
![]()
Полученият резултат показва, че фактическата
оценка на максималното време за превключване на схемата от фигура 4.2.3, е
почти 2 пъти по-малко за достатъчно дълга разрядна мрежа.
Буквалната реализация на изходната структура от фигура
4.2.1 може да бъде оценена по бързодействие по следния начин. Като цяло схемата
е комбинационна, следователно готовите младши цифри от суматор СМ1 постъпват
веднага в суматор СМ2, където в младшите разряди започва събиране с вече
подадените младши цифри на събираемото x1. Искаме да кажем, че превключването
на суматор СМ2 започва със закъснение (3.t) след началото на операцията и протича в по-голямата си част паралелно във
времето с превключването на суматор СМ1. Времевото разположение на двете вериги
от последователно разпространяващи се преноси е изобразено на фигура 4.2.4.
Така, след отчитане на паралелното във
времето функциониране на двата суматора, оценката на времето може да бъде
прецизирана, до следния вид
![]()
Сравнявайки оценката за първоначалната
структура (4.2.6) с оценката на структурата, която беше получена тук (фигура
4.2.3), отчитаме минимална допълнителна преднина от (3.t) секунди.
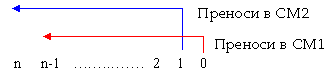
Фиг. 4.2.4. Паралелност във времето
Заключение
В
заключение можем да кажем, че са постигнати положителни резултати, които се
изразяват в следното:
§
Получена е логическа схема, чийто първи етаж е напълно
хомогенен, е с паралелно изчисление и е с максимално възможно бързодействие;
§
Суматорът на втория етаж е типичен, т.е. е с дължината на
операндите;
§
Като цяло схемата е с по-малко време за превключване в
сравнение с последователната.
4.3.
Хоризонтален многовходов суматор
В предходния раздел беше разгледана
възможността за събиране на три числа. В този раздел ще разгледаме
едновременното събиране на повече от три числа. Наименованието на синтезирания
суматор произхожда от интерпретацията на визуалното подреждане на операндите на
входа на суматора.
4.3.1.
Постановка на задачата
Съществуват множество приложни проблеми, генериращи задачата за изчисление
на сума от вида

където
![]()
са означени n-битови числа от един и същ тип и формат.
Като подзадача, сумата (4.3.1) възниква във
векторно-матричните изчисления, в задачите на математическата статистика, в
задачите за цифрова обработка на сигнали и изображения и много други. Идеята за
паралелно събиране по принцип е известна. Тя е актуална в съвременните
изследвания, търсещи бързи апаратни еднотактни и/или конвейерни решения.
Съществуват и различни предложения за структуриране на събирането, но
преобладават такива, които използват тривходови двоични схеми. В същото време
обаче липсват аналитични и сравнителни оценки както и мотиви за предпочитания.
Тук ние представяме една различна и обща апаратната реализация, както и нашето
изследване върху нея.
4.3.2.
Последователно събиране
Класическата двуместна аритметическа операция събиране
![]()
съответства на (4.3.1) и се реализира чрез n-разряден двоичен суматор. Известно е (вижте книга [2]), че възможно най-евтиният и в същото време
най-бърз двоичен комбинационен суматор с последователен пренос, е този с
ускорен последователен пренос. Именно този вид суматор е избран за базов.
Времето за неговото превключване се оценява както следва
![]()
където с t е означено времето за превключване на пълен
едноразряден двоичен комбинационен суматор, а за n се приема че е четно число. Така
задачата за изчисление на сумата (4.3.1) може да бъде решена с помощта на
логическа структура от фигура 4.3.1.
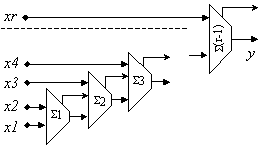
Фиг.4.3.1. Последователно събиране
Въпреки че в показаната структура всички
елементи на сумата са подадени едновременно, всъщност резултатът y
се получава чрез последователно събиране на отделните междинни суми Si с поредния им
текущ операнд xi. При
това всяка от последователните междинни суми, в следствие на възникващия
пренос, е възможно да се удължи отляво максимум с един бит. Така, ако
суматорът S1 е n-битов, то
суматорът S2 следва да бъде (n+1)-битов.
Нататък аналогично следва суматор S3 – (n+2)-битов,
суматор S4 – (n+3)-битов
и т.н. Последният суматор S(r-1) трябва да има дължина (n+r-2) бита.
Очаква се обаче пълноценно събиране в този суматор да се осъществява само в
младшите n
разряда, където се подава последното събираемо xr.
Пълноценно събиране в старшите (r-2)
бита не е възможно. Там е възможно само разпространение и събиране с възможния
пренос от (n-1)-я разряд. Като имаме предвид обаче, че дължината на
събираемите xi е една и съща, вероятността за удължаване на
междинната сума, като резултат на отделните нива в посока към изхода, намалява.
Това означава, че определената по-горе разрядност на последния суматор, е
нереална. Същото се отнася и за дължината на суматорите в по-ниските нива. Не
буди съмнение обаче, че максимално възможната дължина на крайната сума зависи
от броя на събираемите r.
Изявеното несъответствие ни води до следното твърдение.
Теорема
Максимално възможната дължина на сумата от r на брой n-разрядни цели числа
е равна на
![]()
Доказателство
Максимално възможната сума от r на брой еднотипни и
едноформатни числа се получава, когато тези числа имат максимално възможната за
тяхната дължина стойност
![]()
В такъв
случай сумата (4.3.1) от тези еднакви числа може да бъде записана както следва

Най-голямото по стойност число Х
всъщност е двоичен полином от (n-1)-ви ред. В същото време за множимото r в израза (4.3.4) можем
да твърдим, че като двоично число, се намира в границите
![]()
където редът на неговия двоичен полином е q-ти, т.е.
![]()
Така, неизвестното q може да се намери от горното
неравенство, в условията на неизбежен излишък, след логаритмуване
![]()
Известно е, че броят на цифрите в едно число
е с единица по-голям от реда на неговия полином (книга [1]). Така числото r в двоична бройна система ще има (q+1) цифри. В резултат на това следва, че максимално възможната
дължина, необходима за регистрация на максималната r-елементна сума, е
равна на
![]()
което
трябваше да се докаже.
В частния случай, когато
![]()
тогава необходимата дължина за сумата е равна на (n+q).
Така доказаната теорема осигурява реално
необходимата и достатъчна дължина за регистрация на всяка r-кратна сума от вида
(4.3.1). Стойността на изведеното удължение от
(q+1)[b] на разрядната мрежа за резултата е в същото време
минимално необходимото. Сравнявайки резултата от теоремата, с определената
дължина на изходния суматор (n+r-2)[b] в структурата от фигура 4.3.1, ще докажем,
че последната е по-голяма от необходимата.
Това твърдение можем да изразим чрез следното
отношение
n+(q+1)
< n+(r-2) . (4.3.8)
След заместване на q и преобразуване на израза, получаваме
еквивалентното отношение
![]()
Антилогаритмувайки двете части на неравенството,
получаваме следния негов вид
![]()
Последното отношение е вярно за всяко r по-голямо от 6.
Логическата структура от фигура 4.3.1, във
връзка с току що доказаното отношение, може да бъде оптимизирана така, че да
съответства на необходимата и достатъчна разрядност (4.3.3). За целта, ако
дължината на изходния суматор се определя чрез (4.3.3) по силата на доказаната
теорема, същата следва да се приложи за определяне дължината на суматора от
всяко по-долно ниво в структурата. С други думи, за първите (r-1)
събирания, после за първите (r-2) събирания и т.н. В крайна сметка, в
структурата ще има отделни групи от суматори с еднаква дължина, които със
сигурност не генерират старши пренос.
Апаратните разходи за реализация на
структурата представляват сума от разходите за реализация на отделните нива.
Разходите за реализация на суматорите в отделните нива обаче зависи от тяхната
конкретна дължина, която може да се изрази по следния начин
![]()
където с k е изразен номерът на нивото, в което стои поредният
суматор. Така апаратните разходи за реализация на структурата от фигура 4.3.1
могат да бъдат оценени чрез общия брой едноразрядни двоични суматори така
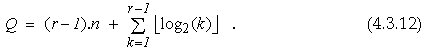
Втората оценка, която ще представим, е
времето за превключване на логическата структура. Като имаме предвид същността
на процеса, който реализира схемата, времето за превключване се определя от
дължината на разпространяващият се в нея пренос. Тъй като преносът се
разпространява по дължината на всеки суматор, а така също по всички нива в
посока към изходното, следва че оценката може да се даде със следната формула
![]()
Следва обаче да отбележим, че тази оценка
(като максимална) не е постижима за всяко r, тъй като преносите са функция на
конкретните събираеми.
4.3.2.
Паралелно събиране
Анализирайки представената на фигура 4.3.1
структура, следва да отбележим, че единственото паралелно събиране в чист вид
се осъществява между числата x1 и x2 в
суматор S1. Всички останали числа – x3,
x4, x5, …, xr практически се натрупват в крайната сума
последователно. Преследвайки поставената в нашето изследване цел за повишаване
бързодействието на структурата за събиране, предлагаме паралелната организация
на събирането да бъде разпространена върху всички възможни двойки събираеми. За
това създаваме структурата, представена на фигура 4.3.2.
Както може да се види от схемата, в първия
ред са разположени r/2 на брой двувходови n-разрядни
суматори S0. На втория ред техният брой отново намалява
два пъти, но там суматорите S1 са (n+1)-разрядни. Така неизбежно се налага да се
изгради представеното последователно свързване, което формира пирамидалната
форма на схемата. Броят на нивата в тази пирамида е равен на q, при което
изходният суматор Sq-1 има разрядността (n+q). Заедно
със старшия пренос, този суматор получава
(n+q+1)-разрядния резултат y.
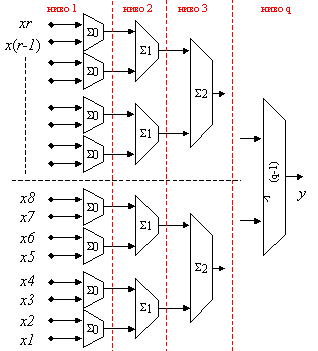
Фиг. 4.3.2. Структура
с паралелно-последователно събиране
Апаратните разходи за реализация на
структурата от фигура 4.3.2 се оценяват аналогично
![]()
където броят на двоичните
суматори в отделните нива се променя както следва
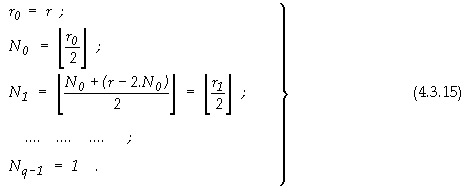
В случай, че броят на събираемите в дадено
ниво е нечетен, останалият елемент, с който е невъзможно да се формира двойка
събираеми, се предава директно към следващото ниво, където заедно с получените
междинни суми, участва във формирането на следващите двойки събираеми. Ето защо
циклическото натрупване ще контролираме чрез условие, зависещо от параметър k, който изразява броя на
нивата в пирамидата.
Според горе записания ред, в общия случай,
броят на двоичните суматори в k-тото по ред ниво на пирамидата, ще се
изрази със следната формула
![]()
![]()
Изчисленията (4.3.16) завършват при условие,
че броят на събираемите в текущото ниво е равен на 1, т.е. когато rk=1. Тогава сумата от
едноразрядни двоични суматори (4.3.14) ще се изрази окончателно с помощта на
(4.3.16) както следва
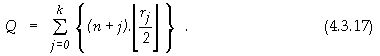
Времето за превключване на структурата от
фигура 4.3.2 се оценява отново чрез дължината на последователно
разпространяващия се пренос при формиране на крайния резултат и при положение,
че суматорите са построени, както приехме по-горе, по схемата с ускорен
последователен пренос. Като имаме предвид, че суматорите в отделните нива
работят паралелно, оценяваме времето за превключване на пирамидалната структура
така
![]()
Сумата отразява дължината на суматорите в
първото ниво, които предават получените цифри към следващото ниво веднага след
тяхното получаване. Окончателните суми на изхода на второто ниво ще закъснеят
по отношение на началния момент заради допълнителния им старши разряд. Логиката
на това превключване се отнася за всички останали нива.
4.3.3.
Паралелно събиране чрез суматори с 3 входа
За разлика от идеята за недовършеното
триоперандното събиране във вид на концентратор (3:2), в предходния раздел е
предложена и оценена завършената схема на многоразряден суматор като 3-входов
концентратор. Получената схема има структурата, показана на фигура 4.3.3 и я
определяме от тип (3:1). Тъй като тази схема е с един изход, прилагането й в
пирамидални структури минимизира броя на нивата. От друга страна тя минимизира
и броя на регистрите фиксатори в случай на конвейерно организирани структури.
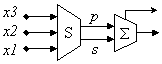
Фиг. 4.3.3. Суматор (3:1)
В тази структура концентраторът S
представлява набор от n
на брой паралелно работещи пълни едноразрядни двоични суматори. Изходната схема
S
представлява пълноценен суматор с дължината на операндите, който събира
поразрядните суми si с поразрядните преноси
![]()
Техническите оценки на представената на
фигура 4.3.3 структура за n-битови двоични числа се дават със следващите
формули. Обемът на апаратните разходи се оценява чрез броя на едноразрядните
двоични суматори
![]()
а времето за превключване –
чрез времето t за превключване на едноразрядния двоичен
суматор
![]()
Вместо паралелното събиране на 2 числа, разгледано
в точка 4.3.2, тук за задачата (4.3.1) ще приложим структуриране на събирането
върху групи от по 3 числа. Прилагането на схемата от фигура 4.3.3 в произволен
случай – r-кратно събиране на n-битови двоични числа, гарантира
минимален брой нива в пирамидалната структура.
Обобщените оценки за такава структура са
изведени с помощта на конкретен пример – 8-кратно събиране на 8-битови числа
(фигура 4.3.4).
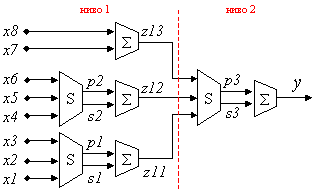
Фиг. 4.3.4. 8-входова
сумираща схема
На първо ниво в структурата, броят на групите
от по 3 събираеми, на които в общия случай се разделя изходното множество от r събираеми, означен с N,
се определя както следва
![]()
Ако по време на групирането остатъкът
![]()
това означава, че е останало едно ненатрупано събираемо. Това събираемо се
подава за групиране по тройки на следващото ниво в пирамидата, заедно с
получените от първо ниво суми (z1)i. В случай че остатъкът е
2, това означава, че са останали 2 ненатрупани събираеми. За тях на текущото
ниво се прилага допълнителен пълноразряден двоичен суматор, какъвто е случаят
на фигура 4.3.4 за събираемите х7 и х8.
При това положение,
оценката на апаратните разходи Q1, в брой едноразрядни двоични
суматори, за реализация на това ниво, в общия случай може да се формализира
така
![]()
![]()
Групирането и реализацията на следващото второ ниво се
извършва по същия начин. Броят на групите от по 3 събираеми N2 се
определя от общия брой на събираемите r2 така
![]()
където общият брой събираеми r2 се определя според
правилото
![]()
![]()
Следва получаване на оценката за апаратните разходи Q2 за
второто ниво
![]()
![]()
За синтеза на произволно по ред ниво, изказаните правила
могат да бъдат обобщени така
![]()
където общият брой събираеми rk+1 се определя според правилото
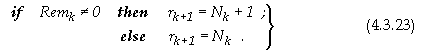
Така оценката за
апаратните разходи Qk-1 ще има вида
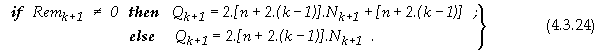
Ако текущото
rk>3, процесът на
синтез на структурата продължава по същия начин. Останалите два случая водят до
последното ниво в пирамидата, което се синтезира както следва:
1.
Ако rk=3, пирамидата завършва със структурата от фигура
4.3.3, какъвто е примерът от фигура 4.3.4, то в този случай апаратните разходи
за последното ниво са
![]()
2.
Ако rk<3, пирамидата завършва само с пълноразряден двоичен
суматор, то в този случай апаратните разходи са
![]()
Отношението rk>3 е в същност условието за
продължаване или за прекратяване на общите правила за синтез на пирамидата. В
крайна сметка общите апаратни разходи представляват сумата от разходите за
отделните нива
![]()
Времето за превключване на структурата от
фигура 4.3.4 при произволен брой събираеми се оценява отново чрез дължината на
последователно разпространяващия се пренос при формиране на крайния резултат и
при положение, че суматорите са построени, както приехме по-горе. Като имаме
предвид, че тривходовите суматори в отделните нива работят паралелно, оценяваме
времето за превключване на структурата чрез следната сума
![]()
Логиката
на това превключване е аналогична на описаната за структурата от фигура 4.3.2.
Заключение
Сравнителните
оценки на апаратните разходи, необходими за реализация на трите структури,
които бяха разгледани по-горе, дадени с формулите (4.3.12), (4.3.17) и
(4.3.25), са представени съответно в таблици 1, 2 и 3, а така също и графично
на фигура 4.3.5. Числените оценки в таблиците са получени за операнди с дължина
n=32[b].
Таблица
4.3.1. Последователно събиране
|
r |
8 |
16 |
24 |
32 |
40 |
48 |
56 |
64 |
72 |
128 |
256 |
|
Qk |
234 |
514 |
802 |
1090 |
1386 |
1682 |
1978 |
2274 |
2578 |
4700 |
9685 |
Таблица
4.3.2. Паралелно събиране
|
r |
8 |
16 |
24 |
32 |
40 |
48 |
56 |
64 |
72 |
128 |
256 |
|
Qk |
228 |
491 |
755 |
1018 |
1283 |
1546 |
1810 |
2073 |
2339 |
4184 |
8407 |
Таблица
4.3.3. Събиране чрез 3-входови схеми
|
r |
8 |
16 |
24 |
32 |
40 |
48 |
56 |
64 |
72 |
128 |
256 |
|
Qk |
228 |
492 |
754 |
1018 |
1282 |
1544 |
1808 |
2073 |
2339 |
4184 |
8410 |
Фиг. 4.3.5. Апаратни
разходи Q в зависимост от броя на събираемите r
Най-съществените
изводи, които се налагат от получените резултати, са:
1.
Разходите
в случаите на паралелна организация са с около 10% по-малки;
2.
Двувходовите
и тривходовите пирамидални схеми се реализират с относително еднакви апаратни
разходи.
Сравнителните
оценки за бързодействието на разгледаните структури, при събиране на 32-битови
числа, въз основа на времето за максимално закъснение при превключване, дадени
с формулите (4.3.13), (4.3.18) и (4.3.26), са представени съответно в таблици
4, 5 и 6, а така също и графично на фигура 4.3.6.
Таблица
4.3.4. Последователно събиране
|
r |
8 |
16 |
24 |
32 |
40 |
48 |
56 |
64 |
72 |
128 |
256 |
|
tΣ |
45.t |
61.t |
77.t |
93.t |
109.t |
125.t |
141.t |
157.t |
173.t |
285.t |
541.t |
Таблица
4.3.5. Паралелно събиране
|
r |
8 |
16 |
24 |
32 |
40 |
48 |
56 |
64 |
72 |
128 |
256 |
1024 |
2048 |
|
tΣ |
34.t |
35.t |
35.t |
36.t |
36.t |
36.t |
36.t |
37.t |
37.t |
38.t |
39.t |
41.t |
51.t |
Таблица
4.3.6. Събиране чрез 3-входови схеми
|
r |
8 |
16 |
24 |
32 |
40 |
48 |
56 |
64 |
72 |
128 |
256 |
1024 |
2048 |
|
tΣ |
34.t |
35.t |
35.t |
36.t |
36.t |
36.t |
36.t |
36.t |
36.t |
37.t |
38.t |
39.t |
39.t |
Фиг. 4.3.6. Време
за превключване tS в
зависимост от броя на събираемите r
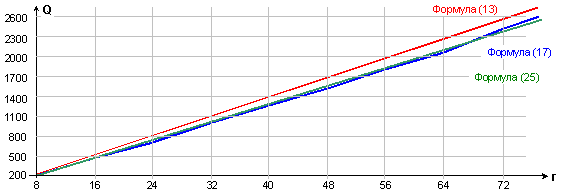
Най-съществените
изводи, които се налагат от получените резултати, са:
1.
Значително
превъзходство на паралелната организация над последователната. Това се дължи на
значително по-малкия брой нива в пирамидалната организация;
2.
Двувходовите
и тривходовите пирамидални схеми имат много бавно разхождащи се отличия в полза
на втората схема. Абсолютната разлика между тях достига до 12 относителни
времеви единици за 2048-кратна сума. В началната част на зависимостите обаче
(например до 128-кратна сума) същите могат да бъдат приети за аналогични (с
точност до 1).
Тук в края ще поясним, че суматорът със
структура, представена на фигура 4.3.2, е наречен “хоризонтален” по причина на
многото операнди, подредени един до друг пред входовете на суматора.
Заключение
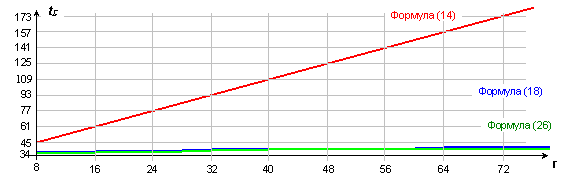
За
потвърждение на получените теоретични оценки за времето за превключване,
представени кратко в таблици 5 и 6, беше организирано експериментално
изследване и сравнение на логическите схеми от фигура 4.3.2 и фигура 4.3.4.
Реализиран е случаят на събиране на 8 двоични числа с дължина 8[b].
Необходимо
е да изтъкнем още като достойнство на схемата от фигура 4.3.4, фактът, че тя,
за разлика от тази на фигура 4.3.2, е в състояние да бъде натоварена с още едно
число. Така тя е в състояние да събира при почти същото апаратно осигуряване и
при същото бързодействие, 9 на брой числа, което схемата от фигура 4.3.2 не
може да осъществи. Реализацията на схемите беше осъществена в ISE-средата
на фирма Xilinx.
При
тези условия оценките за времето за превключване в най-тежкия случай, според
формулите (4.3.18) и (4.3.26) съответно са еднакви
![]() ;
; ![]() .
.
Фиг. 4.3.7. Закъснения в схемата с 2-входови двоични
суматори
Фиг. 4.3.8. Закъснения в схемата с 3-входови двоични
суматори
Като
имаме предвид логическата схема на едноразрядния двоичен суматор, за който
оценката t за
разряди с четен номер е пропорционална на 2 логически елемента, а за разряди с
нечетен номер – на 3 логически елемента, то можем да твърдим, че общото време
за превключване на схемите се намира в интервала [20¸30]
относителни времеви единици. Така изтъкнатите по-горе два теоретични извода са
потвърдени напълно при експериментирането на схемите, което може да се види
по-горе от времедиаграмите на фигури 4.3.7 и 4.3.8.
Както се вижда от времедиаграмите,
закъсненията на двете схеми можем да приемем за еднакви, както и техните
фактически стойности, които са в рамките на 27 относителни времеви единици.
Представените времедиаграми са получени при събирането на следните 8 конкретни
числа
(3+255)
+ (255+0) + (255+0) + (128+129) = (255+255+3) + (0+0+255) + (128+129) =
=
1025 = 10000000001(2).
4.4.
Вертикален многовходов суматор
Прилагайки нашето разбиране за обединяване на операциите,
тук отново разглеждаме операция събиране на повече от три числа. В този раздел
организацията на операцията е различна. Наречена е вертикална, тъй като е
асоциирана с вертикалното подреждане на операндите един под друг, както
обикновено се прави при ръчно събиране.
4.4.1. Постановка на задачата
Постановката на тук изследваната задача е
аналогична на постановката, която е изложена в предходния раздел 4.3. Формално
задачата се изразява така
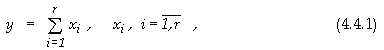
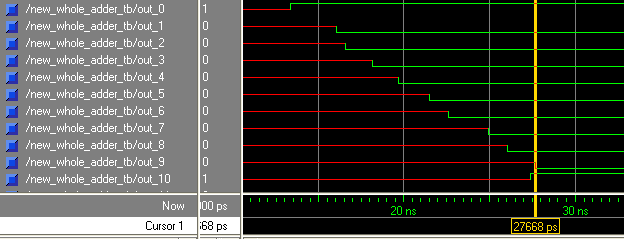
където събираемите х са цели n-битови
числа.
Търсената висока скорост на това изчисление
може да бъде постигната чрез апаратно реализирани логически структури,
характеризиращи се с висока степен на паралелизъм. При тези условия са възможни
два вида организация на изчислението, които се различават помежду си според
първоначалното подреждане на операндите и във връзка с него са именувани
условно “с хоризонтална организация” и “с вертикална организация”. Тук по-долу
е представен синтезът на структура, която реализира “вертикалната” организация.
Изложени са също така направеният за нея анализ, получените количествени
оценки, направените от сравнението на двете структури изводи, както
формулираните общи препоръки за проектиране на апаратни решения, отнасящи се за
разглежданата задача.
4.4.2.
Същност на вертикалната организация
Двоичната аритметична сума от вида (4.4.1)
може да се представи и преобразува чрез полиномния си вид, както следва
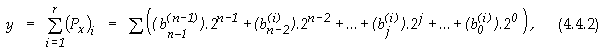
където с
![]()
е означен j-тият бит на i-тото събираемо xi.
Изразът (4.4.2) може да се преобразува във
вида
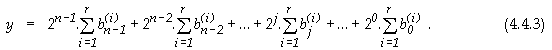
Изразът (4.4.3) може да бъде записан още така
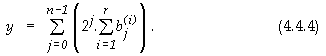
От вида (4.4.4) се вижда, че задачата се разпада на две подзадачи:
1.
Задача
за изчисляване на битовите суми (сума по i ) ;
2.
Задача
за изчисляване на сумата от поразрядно претеглените битови суми (сума по j).
Битовите суми ще бъдат означени така
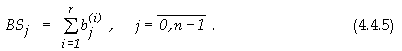
Битовите суми се изчисляват, образно казано,
при вертикално подредени един под друг операнди, така че едноименните им
позиции да застанат една под друга. Това дава наименованието на суматора.
Крайната сума ще се получи като сума от вече получените битови суми, при
спазване на тяхното тегло

Схематично това събиране може да се представи
със следната фигура
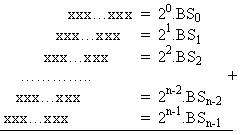
Фиг. 4.4.1. Схема
за събиране на битовите суми
Направеният анализ и формулираните две задачи
са определящи за следващия логически синтез, по време на който се създават две
различни структури, оползотворяващи в максимална степен естествения паралелизъм
на задачите.
4.4.3.
Логическа структура за изчисляване на битова сума
Всички n на брой битови суми BSj
(4.4.5) трябва да се изчислят паралелно във времето, от което следва, че за
целта са необходими n
на брой сумиращи схеми. Това са схеми за паралелно събиране на n на брой еднобитови
числа. В общия смисъл тази задача е аналогична на задачата от предходния
раздел. Това, което я прави по-различна тук, е фактът, че входните операнди са
еднобитови числа.
Преди да представим съображенията за синтез
на логическата структура за получаване на битовата сума, следва да определим
нейната разрядност. Дължината на n-кратната двоична сума от еднобитови
операнди се определя въз основа на доказаната в предходния раздел теорема. Така
за поставената тук задача се получава следното решение в брой битове
![]()
Получената чрез (4.4.7) стойност определя
максимално възможната и достатъчна дължина на двоичната битова сума (4.4.5).
Синтезът на логическата структура за
паралелно събиране на еднобитови числа с използване на концентратори от вида
(3:1), се подчинява на същите съображения, които са изложени в предходния
раздел. Структурата на сумиращата схема е пирамидална (фигура 4.4.2 по-долу), в
която на първо ниво са употребени пълни едноразрядни двоични суматори, което се
дължи на вида на входните операнди. Ако входните операнди са еднобитови, то на
всяко следващо по-високо ниво резултатите увеличават дължината си до
окончателната, изразена чрез (4.4.7).
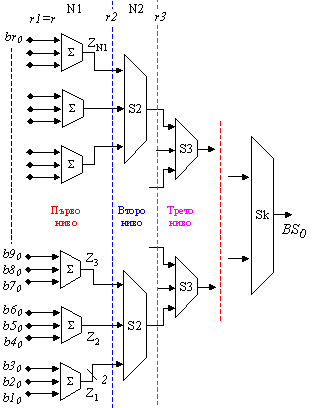
Фиг. 4.4.2. Структура
за изчисляване на битовата сума BS0
За решаваната задача, в таблица 4.4.1 са
представени параметри на възможните за пирамидалната структура суми по нива,
както и техните дължини.
От таблицата може да бъде направен следния
извод: ако броят на числата r
е например 6500, то структурата за получаване на една битова сума ще има 8
нива. Представеното в таблица 4.4.1 води до общия случай за броя на нивата k, като ги свързва с броя
r на входните
операнди
![]()
Сумиращата
схема ще бъде оценена по двата основни критерия: относно обема на апаратните
разходи за нейното реализиране и относно времето за нейното превключване.
Таблица
4.4.1. Възможни за структурата
параметри
|
Ниво № k |
Максимална
стойност на
сумата (Smax) |
Максимална
дължина на сумата
в битове (LBS) |
|
1 |
3 = 31 |
2 |
|
2 |
9 = 32 |
4 |
|
3 |
27 = 33 |
5 |
|
4 |
81 = 34 |
7 |
|
5 |
243 = 35 |
8 |
|
6 |
729 = 36 |
10 |
|
7 |
2187 = 37 |
12 |
|
8 |
6561 = 38 |
13 |
4.4.3.1. Оценка на апаратните разходи
Както се вижда от фигура 4.4.2, в първо ниво
на структурата се намират еднобитови суматори S, чийто брой N1 се определя след
конкретното групиране така
![]()
За остатъка от това групиране
![]()
са възможни две различни от нула стойности (1 и 2). С цел
хомогенизиране на схемата, тези два случая могат да бъдат обобщение в един,
като се приеме, че тяхната сума се получава от един полусуматор. Такъв ще
липсва, ако делението (4.4.9) е точно. Така от първо ниво във всички случаи се
получават r2 на брой 2-битови суми Z=(p,z). В общия случай оценката Q1
на апаратните разходи за това ниво има вида
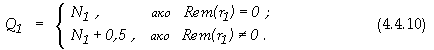
Следващите нива в пирамидалната схема
реализират паралелно-последователно събиране на получените 2-битови числа, чрез
прилагане на концентратори от вида (3:1). Ще обърнем внимание на това, че
максимално възможната 2-битова сума е 3, която в двоична бройна система е
2-цифреното число 11(2),
т.е. (3(10)=11(2)).
Тъй като броят на операндите за второто ниво
е равен на броя на суматорите от първото ниво, то броят на получените 2-битови
числа е
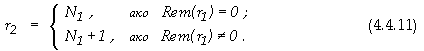
Получените от първо ниво суми се групират по
тройки при съображенията, изложени в предходния раздел, от където следва, че
броят N2 на необходимите за второ ниво концентратори S2, се
определя както следва
![]()
Остатъкът от групирането по тройки Rem(r2)
![]() се оползотворява в
текущото ниво, само ако може да се използва пълен суматор, т.е. когато остават
2 събираеми. В случай, че остава само едно число, то се пренася за групиране
към следващото по-високо ниво. Максимално възможната сума от 3 2-битови числа е
9 (1001(2)), т.е. 4-битово число. Ако отбележим текущото ниво с p, то дължината на
получаваните на това ниво суми Lp, може да бъде се изчислена
така
се оползотворява в
текущото ниво, само ако може да се използва пълен суматор, т.е. когато остават
2 събираеми. В случай, че остава само едно число, то се пренася за групиране
към следващото по-високо ниво. Максимално възможната сума от 3 2-битови числа е
9 (1001(2)), т.е. 4-битово число. Ако отбележим текущото ниво с p, то дължината на
получаваните на това ниво суми Lp, може да бъде се изчислена
така
![]()
Получената оценка за дължината на сумата
позволява да бъдат оценени апаратните разходи за концентраторите в същото ниво,
както следва
![]()
Така оценката за обема Q2
на апаратните разходи при реализиране на второ ниво, в брой едноразрядни
двоични суматори, в общия случай, е следната
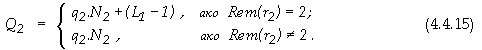
Броят на получените от второ ниво суми е
означен с r3. Точният им брой се определя по следния начин
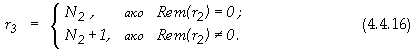
Максималната дължина на двоичните суми на
изхода на второ ниво, е L2=4 бита. Върху тези числа се
прилага групиране по тройки и се формира третото ниво концентратори S3. Техният
брой се определя аналогично
![]()
Дължината на сумите L3,
които ще се получат на това ниво, се определя според зависимостта (4.4.13), а
разходите q3 за един концентратор с тази дължина се определя
според зависимостта (4.4.14). Апаратните разходи за реализация на цялото трето
ниво се оценяват както следва
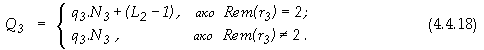
За синтеза на
произволно по ред ниво, по индукция върху изказаните по-горе оценки, са
направени следните обобщения:
1. Относно
дължината на единична сума, получавана на текущото ниво №p
![]()
2.
Относно оценката на апаратните разходи за единичен концентратор в
текущото ниво
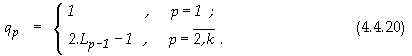
3.
Относно броя на необходимите за текущото ниво №p концентратори

4.
Където общият брой събираеми rp се определя както следва
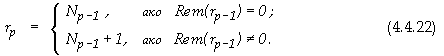
5.
Относно обема на апаратните разходи за реализация на текущото ниво №p
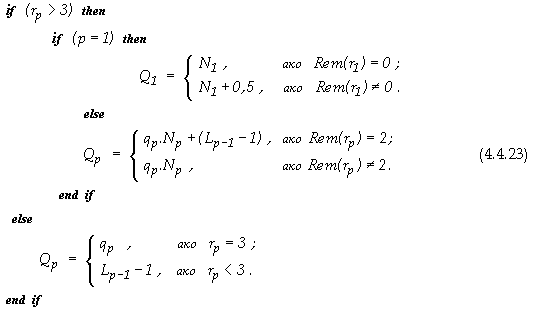
6.
Относно условието за продължение
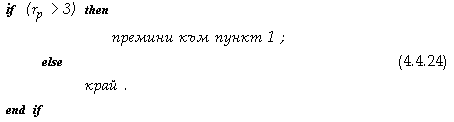
В крайна сметка, общите апаратни разходи за
реализация на структурата от фигура 4.4.2, се оценяват със следната сума
![]()
а разходите за паралелното получаване на всички n
на брой битови суми (4.4.5), се оценяват с израза
![]()
4.4.3.2.
Оценка на времето за превключване
Тъй като битовите суми се изчисляват от
паралелно работещи схеми, то необходимото за това време, се определя от времето
за превключване на логическата структура от фигура 4.4.2. Времето за нейното
превключване се оценява при същите условия, които са приети в предходния
раздел, и като се има предвид, че входните операнди са еднобитови числа,
окончателната оценка на времето за превключване на тази структура получава вида
![]()
4.4.4.
Изчисляване на сумата от битовите суми
Тази сума се представя от израза (4.4.6),
която във връзка с групирането по тройки, може да бъде преобразувана във
следния вид
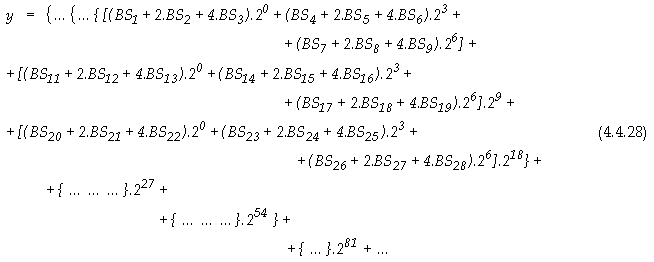
От този запис, както и от фигура 4.4.1, се вижда, че
сумата y от последователно изместените една спрямо друга битови суми BS,
може да бъде натрупана в процеса на паралелно-последователно събиране с
изместване и прилагане на концентратори от типа (3:1), както е показано на
фигура 4.4.3.
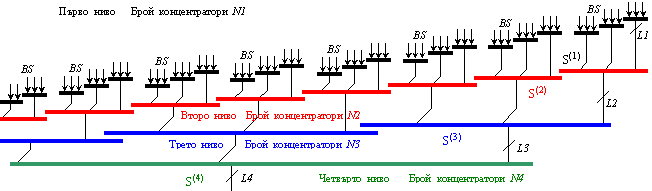
Фиг. 4.4.3. Пирамидална
структура за паралелно събиране на битовите суми
Необходимо е да поясним, че поради силното
удължаване, фигура 4.4.3 илюстрира само част от общата схема, т.е. само
младшата част.
Заради взаимното относително изместване
наляво на събираемите от дадена група, синтезът на концентраторите в отделните
нива се различава и ще бъде описан в следващия раздел.
Паралелно-последователната структура също трябва да се изгради от
концентратори, при синтеза на които трябва да бъдат отчетени различните
условия, създавани при преход към по-високо ниво. От една страна, това е
променливата стъпка на относителното изместване, а от друга страна,
променливото удължаване на сумите, което е свързано с изместването.
Така например, концентраторите на първо ниво
събират по три битови суми BS, които са изместени една спрямо друга на 1
бит. Концентраторите на второ ниво събират по тройки сумите S(1),
получени от първо ниво, но с относително изместване една спрямо друга на 3 бита,
т.е. с относителни позиционни тегла 20, 23, и 26
(вж. израза (4.4.28)). Концентраторите на трето ниво събират по тройки сумите S(2),
получени на второ ниво, но взаимно изместени на 9 бита (20, 29,
218). Така относителните измествания на входовете на съответните
концентратори нарастват последователно в геометрична прогресия: 1, 3, 9, 27, …
От своя страна разрядността на междинните резултати също
нараства в посока на изхода. Тъй като всички концентратори събират по три
числа, тяхното удължаване отляво зависи най-вече от относителното изместване
един спрямо друг на входните им операнди. Следователно, за да се оцени
логическата структура от фигура 4.4.3, трябва да бъдат отчетени всички горе
изложени съображения.
Броят на нивата в пирамидалната структура от
фигура 4.4.3 се определя от броя на битовите суми, т.е. от разрядността n
на дадените операнди, както и от методиката за групиране по тройки, според
която, остатъкът от групирането (Remk=0,1,2), се прехвърля за
групиране в по-високото ниво. В таблица 4.4.2 са представени конкретни
резултати за броя на концентраторите по нива, в зависимост то дължината на
операндите – 8-битови, 16-битови, 32-битови и т.н. до 256-битови.
Таблица 4.4.2. Брой на концентраторите по нива
|
Брой на концентраторите N по нива |
Брой на битовите суми (n= ) |
|||||
|
8 |
16 |
32 |
64 |
128 |
256 |
|
|
N1 |
2 |
5 |
10 |
21 |
42 |
85 |
|
N2 |
1 |
2 |
4 |
7 |
14 |
28 |
|
N3 |
1 |
1 |
1 |
2 |
5 |
10 |
|
N4 |
0 |
0 |
1 |
1 |
2 |
3 |
|
N5 |
0 |
0 |
0 |
1 |
1 |
1 |
|
N6 |
0 |
0 |
0 |
0 |
0 |
1 |
В разглеждания тук случай, оценката на
апаратните разходи се различава и усложнява в сравнение с разгледаните досега,
поради индивидуалното по нива относително изместване на операндите, както и
поради променящата им се дължина. Така се обособява като самостоятелна задачата
за определяне дължината на концентраторите по нива.
4.4.3.3.
Оценка на апаратните разходи
На първо ниво всеки концентратор събира три
последователни битови суми, които са изместени една спрямо друга на 1 бит.
Независимо каква е тяхната разрядност LBS (4.4.7), дължината на сумите S(1)
в първо ниво (вж. фигура 4.4.3) се определя от илюстрираната на фигура 4.4.4
схема
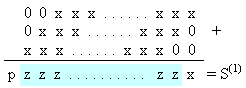
Фиг. 4.4.4. Събиране
в концентратор на първо ниво
От илюстрацията се вижда, че дължината на
двоичните суми, които се получават от концентраторите на първо ниво, може да се
изрази както следва
![]()
Апаратните разходи QS1 за
концентраторите, реализиращи сумите от фигура 4.4.4, се определят при следните
съображения:
1.
Операция
събиране в младшия разряд фактически не се изпълнява;
2.
Сумата
в следващия по-старши разряд може да се реализира с полусуматор;
3.
Чрез
полусуматор могат да се реализират двата най-старши бита на резултата;
4.
По-младшият
от тях разряд може да се реализира чрез пълен едноразряден суматор.
Така оценката на апаратните разходи за един
концентратор от първо ниво, в брой едноразрядни двоични суматори, се изразява
със следния израз
![]()
Общите апаратни разходи за реализация на първо
ниво се определят така
![]()
където общият брой концентратори N1 се определя от
методиката за групиране по тройки.
На второ ниво всеки концентратор събира три
суми S(1), изместени една спрямо друга на 3 бита. Фигура 4.4.5
илюстрира схемата на събирането
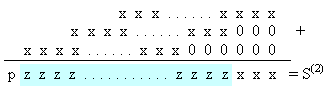
Фиг. 4.4.5. Събиране
в концентратор на второ ниво
Разрядността на получаваните
на второ ниво суми S(2) се
определя чрез израза
![]()
Апаратните разходи QS2 за
концентратори, реализиращи суми S(2), се определя въз основа на
аналогични съображения, изказани по-горе. Крайният вид на тази оценка има вида
![]()
Общите апаратни разходи за реализация на
второ ниво се определят така
![]()
На трето ниво всеки концентратор събира три
суми S(2), изместени една спрямо друга на 9 бита. Разрядността на
получаваните на трето ниво суми S(3) се определя чрез израза
![]()
Апаратните разходи QS3 за концентратори, реализиращи суми S(3), се
определя въз основа на аналогични съображения, изказани по-горе. Крайният вид
на тази оценка има вида
![]()
Общите апаратни
разходи за реализация на трето ниво се определят така
![]()
Изложеният до момента последователен анализ е достатъчен,
за да може чрез метода на индукцията да се обобщят оценките за дължината на
двоичните суми, за апаратните разходи, необходими за реализация на един
концентратор, както и на общите за произволно ниво апаратни разходи. Необходимо
е да се поясни обаче, че според методиката за групиране, оценките (4.4.31),
(4.4.34) и (4.4.37) са валидни, само ако
остатъците от групирането са нулеви. В случай, че остатъкът е единица (Remk=1),
останалото негрупирано число се пренася за групиране в следващото ниво. Ако
остатъкът от групирането на входните за текущото ниво операнди е Remk=2, то в това ниво се
добавя двоичен суматор, който ще събира тези 2 останали числа, с отчитане на
взаимното им изместване. Апаратните разходи за този допълнителен суматор следва
да се добавят към общите разходи за текущото ниво. Така, в общия случай, когато
остатъкът е различен от нула, броят на входните операнди за следващото ниво се
увеличава с единица.
Апаратните разходи за реализация на споменатия
допълнителен суматор зависят от дължината на взаимното изместване и от
дължината на операндите. Общата формална оценка на разходите за този суматор се
определя като се отчете фактът, че в младшите mk разряда
фактическо събиране липсва, а в старшите mk разряда е
възможно само разпространение на пренос. Пълноценно събиране се изпълнява само
в средните разряди, а именно от разряд
№(mk) до
разряд (LSk-1-mk).
По този начин може да се обобщи оценката за апаратните разходи за този вид
суматори до следния вид
![]()
И
така, получените общи оценки имат следния вид:
1.
За
дължината m на
взаимното изместване на операндите за следващото ниво, като функция от номера k на нивото
![]()
2.
За
дължината на получаваните суми, функция от номера k на нивото
![]()
Горната
формула може да се опрости до следния вид
![]()
3.
За
обема на апаратните разходи, реализиращи един концентратор, като функция от
номера k на
нивото
![]()
4.
За
обема на апаратните разходи на k-тото ниво
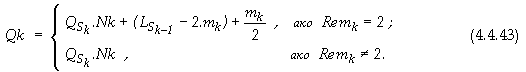
където общият брой концентратори Nk се определя
чрез методиката за групиране по тройки, изразена чрез (4.4.21) и (4.4.22). Условието
за край на итерационния процес, според който се синтезира тази логическа
структура, е аналогично на (4.4.24).
5.
За
обема на общите за тази задача апаратни разходи
![]()
6.
Сумата
от оценките (4.4.26) и (4.4.44) определя обема на общите за задача (4.4.1)
апаратни разходи за разглеждания тук вариант на вертикална организация.
На фигура 4.4.6 е показан графичният вид на
сумата от оценките (4.4.26) и (4.4.44) като функция от броя r на събираемите, ако в
частност те са: 8 битови числа (•••); 16 битови числа (•••) и 30 битови
числа (•••).
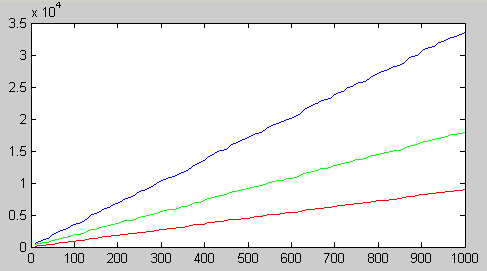 r
r
Фиг.
4.4.6. Обемът на апаратните разходи Q като
функция от броя на числата (в интервала от 10 до 1000)
4.4.3.3.
Оценка на времето за превключване
Оценката на общото време за превключване на
синтезираната структура се получава като се отчете факта, че тя се състои от
две последователни части – n на брой паралелно работещи структури, изчисляващи
битовите суми, с последваща “хоризонтална” структура за тяхното паралелно
събиране. Така се стига до формулата
![]()
където оценката за превключване на “вертикалната”
(4.4.27) и на “хоризонталната” структури съответно имат вида
![]()
Както се вижда, дължината на битовите суми LBS е взета на половина, отчитайки по този начин
взаимното изместване на операндите на входа на концентраторите във втората
структура.
На фигура 4.4.7 графично е представен вида на
оценката (4.4.45) като функция от броя r на събираемите, ако в частност те са: 9 битови числа (•••); 17 битови
числа (•••) и 33 битови числа (•••).
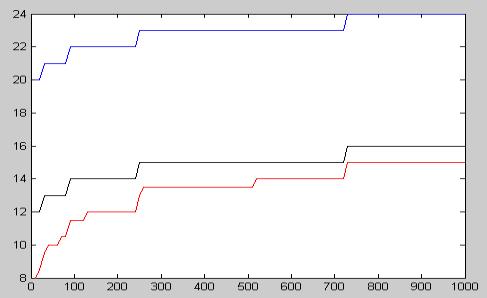 r
r
Фиг. 4.4.7. Времето
за превключване tS като функция от броя на числата (в интервала
от 10 до 1000)
Заключение
Изследваният тук алтернативен “вертикален” вариант за
организация на паралелно събиране на много числа, заедно с “хоризонталния”
вариант за организация, изцяло изчерпва поставената задача (4.4.1). Получените
за двата варианта резултати са сравнени, а направените изводи, са кратко
представени по-долу.
1.
Апаратните
разходи (за реализация на синтезираната тук логическа структура) линейно
нарастват с нарастване броя на събираемите.
2.
Основната
част (над 95%) от апаратните разходи за структурата с вертикална организация се
падат на подструктурата за изчисляване на битовите суми.
3.
Подструктурата
за изчисляване на битовите суми се характеризира с висока степен на
хомогенност, тъй като е съставена от n на брой паралелно работещи еднакви схеми. В
този смисъл, като цяло, реализацията на вертикалната структура може да бъде
адаптирана по-бързо при изменения в параметрите на задачата.
4.
Апаратните
разходи за реализация на двете алтернативни организации (хоризонтална и
вертикална) са еквивалентни при едни и същи параметри на задачата (1).
5.
Поставен
е въпросът: могат ли да бъдат сравнявани двете структури при различни параметри
на задача (4.4.1)? Или с други думи – коя структура следва да се предпочете,
ако числата са например много на брой, но с малка дължина, или са малко на
брой, но са с голяма дължина? Като условие за еднаквост при сравнение на получените
оценки е възприето приблизителното равенство между модулите на крайните суми.
Така например, при n=8 и r=643, максималната сума е Xmax=643.255=163965.
Приблизително същия резултат (Xmax=10.16383=163830) има задачата с параметри: n=14 и r=10. Отговорът на
въпроса е: тъй като апаратните разходи за вертикалната и за хоризонталната
структури и за двата случая са еквивалентни, по този критерий не може да се
формулира предпочитание.
6.
Представеният
на фигура 4.4.7 интервал на аргумента r позволява да се забележи
експонентна тенденция в нарастването на времето за превключване.
7.
Сравнението
на времената за превключване на структурите за примера от извод №5 позволява да
се направи следния извод: при еднакви параметри на задача (4.4.1), времето за
превключване на вертикалната структура е еквивалентно с времето за превключване
на хоризонталната структура, ако параметрите са в съотношението r>>n. Когато обаче
съотношението е обратно (r<<n),
времето за превключване на вертикалната структура е повече от два пъти по-добро
в сравнение с това на хоризонталната структура.
Примери
Пример №1:
Дадени са 643 на брой 8-битови числа, т.е. r=643, n=8[b].
Xmax = 643.255 = 163965 . Тази
стойност може да се представи в 18 битово поле, което се определя според
формулата
![]() .
.
Задача 1. Оценка
на апаратните разходи за изчисление на битовите суми.
На първо ниво (p=1) се получават 2-битови суми (L1=2[b]). Апаратните
разходи за един концентратор са q1=1.
Броят на необходимите суматори е N1=214 с остатък
Rem1=1. Общите апаратни разходи за първо ниво са Q1=214,5. Броят на
операндите за следващото второ ниво е r2=215.
На второ ниво (p=2) се получават 4-битови суми (L2=4[b]). Апаратните
разходи за един концентратор са q2=3.
Броят на необходимите концентратори е N2=71 с остатък
Rem2=2. Общите апаратни разходи за второ ниво са Q2=3.71+(2-1)=214. Броят
на операндите за следващото трето ниво е
r3=72.
На трето ниво (p=3) се получават 5-битови суми (L3=5[b]). Апаратните
разходи за един концентратор са q3=7.
Броят на необходимите концентратори е N3=24 с остатък
Rem3=0. Общите апаратни разходи за трето ниво са Q3=7.24=168. Броят на
операндите за следващото четвърто ниво е
r4=24.
На четвърто ниво (p=4) се получават 7-битови суми (L4=7[b]). Апаратните
разходи за един концентратор са q4=9.
Броят на необходимите концентратори е N4=8 с остатък
Rem4=0. Общите апаратни разходи за четвърто ниво
са Q4=9.8=72. Броят
на операндите за следващото пето ниво е
r5=8.
На пето ниво (p=5) се получават 8-битови суми (L5=8[b]). Апаратните
разходи за един концентратор са q5=13.
Броят на необходимите концентратори е N5=2 с остатък
Rem5=2. Общите апаратни разходи за пето ниво са Q5=13.2+(7-1)=32. Броят на
операндите за следващото шесто ниво е r6=3.
Последно е шесто ниво (p=6), на което се получава
окончателният 10-битов резултат (L6=10[b]).
Апаратните разходи за един концентратор са
q6=15. Общите апаратни разходи за последното шесто
ниво са Q6=15.
Общите апаратни разходи за реализация на една
битова сума чрез сумата:
QBS
= Q1+Q2+Q3+Q4+Q5+Q6 = 214,5+214+168+72+32+15 =
715,5.
Така разходите за всички 8 на брой битови
суми съставят стойността:
Q
= 8.715,5
= 5724.
Задача 2. Оценка на апаратните разходи за изчисление сумата от битовите суми.
За разглеждания пример битовите суми са 8 на
брой, всяка от които представлява 10-битово число. На първо ниво в
пирамидалната сумираща структура осемте битови суми се групират последователно
по тройки с взаимно изместване на 1 бит. Необходимите за това ниво
концентратори са N1=2 (остатък Rem1=2). Апаратните
разходи за реализация на това ниво се определят според (4.4.43). За целта,
според (4.4.41), се определя дължината на получаваните суми, а според (4.4.42)
– разходите за един концентратор. Останалите 2 числа се събират в един двоичен
суматор с взаимно изместване на 1 бит. Разходите за този суматор според
(4.4.42) се оценяват на
![]()
Броят на числата, които постъпват на второ
ниво е 3, по тази причина то е последно. Числата се събират с един концентратор
при взаимно изместване на 3 бита.
Дължината на сумите, получавани от първо
ниво, е LS1=10+3=13[b].
Разходите за един концентратор, са QS1=2.(10-1)=18.
Тъй като на първо ниво концентраторите са 2, то общите разходи за това ниво,
заедно с допълнителния суматор, са Q1=2.18+8,5=44,5. Двете най-старши битови суми с отместване на
6 и на 9 бита се подават за събиране към второ ниво.
На второ ниво се групират по тройки общо 3
числа – 2 суми от вида S1 и една сума å1. Става ясно, че това ниво е последно.
Сумата S2, получена на второ ниво, има според (4.4.27) дължината LS2=13+1.3+0=16[b].
Изчислената дължина отчита факта, че третото събираемо е 10-битово число,
изместено на 2.3=6 бита. Разходите за концентратора на второ ниво се оценяват
според (4.4.28) на
Q2 =
2.(13-2.3)+1.3+0 = 2.7+3
= 17.
Общите разходи се представят от сумата
Q = Q1+Q2 =
44,5+17 = 61,5 .
В крайна сметка за цялата задача апаратните
разходи се представят от сумата
Q = 5724+61,5
= 5785,5.
Оценката при хоризонтално събиране е:
Q = 3424+1430+528+224+80+36 = 5722 .
Както се вижда, разликата е 5785,5-5722=63,5,
която е около 1,1% в полза на хоризонталното събиране.
Числените стойности на оценките на времето за
превключване са следните
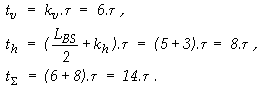
В същото време конкурентната хоризонтална
структура има следната стойност на времето за превключване
![]()
Пример №2:
Дадени са 10 на брой 14-битови числа, т.е. r=10, n=14[b].
Xmax = 10.16383 = 163830 .
Както се вижда, числата са подбрани така, че
крайната сума в двата примера да е почти едно и също число (разлика от 135
единици или още 0,8%), което означава, че за неговото представяне е необходимо
едно и също двоично поле.
Задача 1. В
този пример битовите суми са 14 на брой.
На първо ниво (p=1) се получават 2-битови суми (L1=2[b]). Апаратните
разходи за един концентратор са q1=1.
Броят на необходимите суматори е N1=3 с остатък
Rem1=1. Общите апаратни разходи за първо ниво са Q1=3,5. Броят на
операндите за следващото второ ниво е r2=3.
Останалият еднобитов операнд не отчитаме на второ ниво, тъй като ще бъде
прибавен под формата на младши пренос в един от суматорите на второ ниво
На второ ниво (p=2) се получават 4-битови суми (L2=4[b]). Апаратните
разходи за единствения (N2=1)
концентратор са q2=3.
Остатъкът е Rem2=0.
Общите апаратни разходи за второ ниво са
Q2=3.
Общите апаратни разходи за реализация на една
битова сума, се оценяват на
QBS = Q1+Q2 = 3,5+3 = 6,5 .
Общите за всички 14 на брой битови суми
разходи са: Q=14.6,5=91.
Задача 2. Всяка от получените 14 битови суми
представлява 4-битово число. Числата се събират в хоризонтална пирамидална
структура с отчитане на взаимното им изместване.
На първо ниво броят на необходимите
концентратори е N1=4 (остатък Rem1=2).
Дължината на тези суми за примера се определя на LS1=7[b]. Разходите за един концентратор според
(4.4.25), са QS1=2.(4-1)=6.
На първо ниво концентраторите са 4. Останалите 2 най-старши битови суми,
взаимно изместени на един бит, се събират в двоичен суматор, разходите за който
се оценяват на
![]()
Дължината на тази сума е не повече от 9 бита.
Общите за първо ниво разходи съставят сумата:
Q1 = 4.6+3,5 = 27,5.
На второ ниво се групират по тройки общо 5
числа с взаимно изместване на 3 бита. За тяхното паралелно събиране са
необходими един концентратор и един суматор. Дължината на получаваните от второ
ниво суми е
LS2 =
7+2.3+1 = 14[b].
Разходите за концентратора се оценяват на
QS2 =
2.(7-2.3)+2.3+1 = 9, а
разходите за суматора – на QS2
= (7-2.3)+1,5 =
2,5.
Така общите разходи за реализация на второ
ниво съставят сумата
Q2 =
1.9+2,5 = 11,5.
На трето ниво един двоичен суматор събира
двете суми от второ ниво, взаимно изместени на 9 бита. Едната сума е 14 битова
а другата 9 битова, така че дължината на окончателния резултат не е по-голяма
от 18[b]. Апаратните разходи за този суматор са: QS3
= (14-9)+2 = 7.
Разходите за реализация на втората
пирамидална структура се получава като сума от горе изчислените разходи
Q = Q1+Q2+Q3 =
27,5+11,5+7 = 46 .
Общите разходи за реализация на този пример
във варианта на вертикално събиране съставят сумата
Q = 91+46
= 137 .
Оценката при хоризонтално събиране е:
Q =
84+30+18 = 132 .
Както се вижда, разликата е само 5
относителни единици, която е около 3,8% в полза на хоризонталното събиране.
Числените
стойности на оценките на времето за превключване за този пример са следните
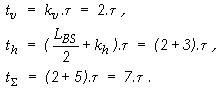
В същото време конкурентната хоризонтална
структура има следната стойност на времето за превключване
![]()
4.5.
Оценка на производителността при конвейерна организация на изчисленията
Вече имахме повод да разглеждаме понятието
производителност, за което в глава 2 беше изведена оценката (2.1.3). Според
тази оценка, производителността на един m-степенен синхронен конвейер е m пъти по-висока в
сравнение с обикновения последователен ход на изчислителния процес. Но както
вече читателят е разбрал, тук разглеждаме значително по-сложни условия на
конвейерната организация. Последната се характеризира най-вече като асинхронна,
за която многократно твърдяхме, че води към по-висока производителност. Така
въпросът за оценка на производителността се повдига отново и напълно оправдано,
ето защо този раздел е посветен на нея.
Разглеждаме m-степенен микроконвейер (фигура
4.5.1), представляващ хардуерна реализация на изчислителен процес с линейна
алгоритмична структура.
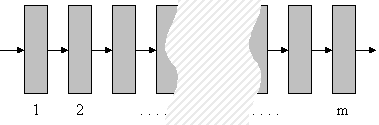
Фиг. 4.5.1. Линеен микроконвейер
Микроконвейерът е съставен от m на брой последователно свързани
микроконвейерни звена, всяко едно от които реализира една математическа
операция върху данните, предавани между звената.
Изчисленията, реализирани по този начин, следва да бъдат
многократно изпълнени върху различни входни данни. Всяко отделно изчисление,
което се изпълнява по дадения алгоритъм, ще наричаме тук задача. Така в
разглежданото изчислително средство трябва да бъдат изпълнени n на брой задачи.
Въпросът е, как е възможно това да бъде организирано изчислението и за колко
време ще бъдат изпълнени тези изчисления, което е съществото на задачата за
оценка на производителността.
Възможности за организация
Възможностите за организация на изчисленията при
множество задачи са две:
1.
Последователно (не
конвейерно) изпълнение на задачите, при което нова задача постъпва в изчислителното
средство след получаване на резултата от предидущата задача, т.е. след
приключване на изчисленията по нея;
2.
Паралелно
(конвейерно) изпълнение на задачите, при което всяка нова задача постъпва в
изчислителното средство веднага след като входното микроконвейерно звено се
освободи.
При конвейерната организация изчислителният процес се
постига като входните данни и междинните резултати се прехвърлят от звено към
звено. Има се предвид, че според алгоритъма изчисленията са последователност от
операции, всяка една от които се изпълнява в съответното конвейерно звено. В
този смисъл, когато едно звено предаде своя резултат на следващото, то се счита
за свободно и може да приеме нови данни, върху които ще изпълни същите
изчисления.
Всяка една от тези организации може да прилага някой от
следните методи за управление на данновия трансфер между микроконвейерните
звена:
1.
Синхронен, при
който за управление на данновия трансфер се използват правоъгълните импулси на
тактов сигнал с постоянна честота. Периодът на тактовата честота трябва да бъде
достатъчно продължителен, щото всяко конвейерно звено да успява да изчисли своя
резултат и да гарантира по този начин, че следващото звено ще получи правилен
резултат;
2.
Асинхронен. При
този метод на управление данновия трансфер между конвейерните звена се
управлява от конвейерни автомати, по силата на принципа на
самосинхронизирането.
При тези условия тук е поставена задачата за оценка на
производителността на изчислителното средство при различните организации за
функциониране, както беше определено. Производителността ще оценяваме чрез
времето, необходимо за изпълнение на един и същ брой задачи. Нещо повече, в
крайна сметка се интересуваме кой от вариантите печели състезанието и с колко.
С цел да се ограничим относно многообразието на
възможностите и да получим в първо приближение оценки, които да ни позволят да
направим заключителните изводи, ще се придържаме към типичните възможно
най-добри условия на функциониране. Така например първоначално ще приемем, че
времето за изчисление във всяко конвейерно звено, е приблизително едно и също,
което за един конвейер е най-добрата ситуация, тъй като тогава темпът на
функционирането му ще бъде равномерен. Това от своя страна означава, че
най-евтиното управление на данновия трансфер ще бъде синхронното с постоянна
честота.
Случай 1.
Последователно (не конвейерно) синхронно управление
В този случай се има предвид класическа организация на
управлението чрез управляващ краен автомат, тактуван с постоянна честота.
Периодът Т на тази честота ще се избира така, че да бъде достатъчен за
изчисленията във всеки един такт, т.е. това е време, достатъчно за ичисленията
във всяко едно от операционните звена. При последователно (не конвейерно)
организирано изчисление, времето, необходимо за решаване на една задача
представлява сума от отделните тактове на управляващия алгоритъм. При тази
постановка ще бъдат необходими m такта, т.е. времето ще бъде m.T секунди. Тогава
последователното изпълнение на n на брой задачи ще отнеме
![]()
Случай 2.
Паралелно (конвейерно) синхронно управление
За повишаване на производителността се въвеждат различни
форми на паралелизъм в организацията на изчисленията. Основната форма, която
масово се практикува, е конвейерната. Така конвейерната организация на функционирането,
при m
степенен конвейер, позволява едновременна обработка на m брой задачи. В
условията на равномерен темп, които бяха приети в началото тук, необходимостта
от управляващ краен автомат отпада и то се постига чрез непосредствено
използване на тактовата последователност. Тактовите импулси се подават
едновременно към всички микроконвейерни звена за да реализират данновия
трансфер между тях.
При конвейерна организация, в изчислителната структура
последователно на всеки такт се зарежда нова задача. Така, когато първата
заредена в конвейера задача постъпва в последното му звено, във входното ще
постъпи m-тата. За да се запълни конвейера с тези m на брой задачи са
необходими m
такта. Времето, необходимо за изпълнение на така заредените в конвейера задачи,
ще бъде
![]()
Ако броят на задачите трябва да бъде голям, т.е. n >> m, и може да се раздели на k групи от по m задачи, то
необходимото за изпълнението им време, ще бъде следното
![]()
Броят на групите, на които се разделя общият брой задачи,
се определя както следва
![]()
За да улесним изчисленията, ще приемем, че n е кратно на m, при което след
заместване на k
в (4.5.3), ще получим
![]()
Конвейерната организация на функциониране се определя
като по-високо производителна. Повишението на производителността на този вид
организация в сравнение с предходната може да се измери (при еднакви условия)
чрез отношението на изразходваното време за решаване на задачите
![]()
Така, ако означим степента на повишение на производителността с Р,
то в този случай тя ще се оценява с отношението
![]()
За горната оценка твърдим, че има стойност,
която клони към числото m,
с нарастване на броя на изпълнените задачи
Резултатът означава, че m-степенната
синхронна конвейерна организация е m пъти по-производителна от еднозадачната
последователна синхронна организация на изпълнение на целия набор от задачи.
За нас обаче по-интересен е случаят на асинхронно
управление, който първоначално ще разгледаме при последователно и не конвейерно
функциониране.
Случай 3. Последователно (не конвейерно)
асинхронно управление
Според модела на фактическото закъснение, изчислението в
едно микроконвейерно звено се ограничава във времевия интервал [tmin,
tmax]. Реалното закъснение ti на i-тото звено
зависи от входните данни и за всяко ново изчисление то е различно и в този
смисъл има случаен характер. Ако интерпретираме закъснението t като случайна величина,
ще приемем в първо приближение, че закона на нейното разпределение е нормален.
Параметрите на това разпределение N(μi , σi)
– средна стойност mi и средно квадратично отклонение si могат да бъдат оценени така:
![]()
При тези оценки е отчетено ограничението, което налагат
границите на затворения интервал, в който се намира всяка реална стойност на
закъснението t.
Закъснението, с което се получава крайният резултат на
една задача, преминала през всички m звена на конвейера, е сума от закъсненията
на отделните звена. Тези закъснения са различни, но както вече приехме, се
изразяват чрез нормалния закон на своите разпределения. Общото закъснение на
конвейера при изпълнение на една задача ще бъде

Можем още да приемем, че отделните закъснения ti
са независими случайни величини, от което следва (по силата на теоремата за
големите числа), че тяхната сума (4.5.10) е случайна и нормално разпределена
величина с параметри
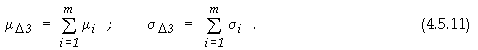
За да облекчим изчисленията и сравнението, въпреки
реалностите на хардуера ще приемем още, че минималните закъснения могат да
бъдат нулеви (tmin ³ 0), а максималните не могат да бъдат по-големи от
периода за тактуване Т (tmax £ T). Основание за това намираме в приетото положение, че
темпът на функциониране на конвейера е възможно най-добрия, т.е. той е
равномерен. При това периодът Т при синхронното управление се избира да не бъде
по-малък от максимално възможното закъснение. С други думи приемаме за
фактическото закъснение на всички конвейерни звена интервала (0,Т]. От тук следва, че оценките за
отделните звена ще бъдат
![]()
и съответно
оценките за целия конвейер (при ![]() )
)
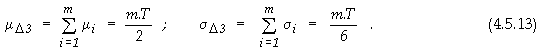
Сега вече можем да съпоставим оценките (4.5.1) и (4.5.10)
като по този начин оценим степента на повишение на производителността.
Съпоставянето е при еднакви условия – n на брой задачи, зареждани последователно и
изпълнявани не конвейерно. Времето за изпълнение в първия случай е D1. Времето за изпълнение на същия брой задачи в конвейер с асинхронни
микроконвейерни звена е случайна величина, но нейната най-вероятна стойност е ![]() . Тогава, образувайки отношението
. Тогава, образувайки отношението
![]()
стигаме до извода,
че при последователно изпълнение на задачите и при управление на конвейера с
асинхронен краен автомат, който реализира модела на фактическото закъснение,
най-вероятно ще бъде постигната най-малко двойно по-висока производителност в
сравнение със синхронно управлявания конвейер.
Случай 4.
Паралелно (конвейерно) асинхронно управление
В тази разновидност на управлението, изпълнението на
задачите ще бъде организирано напълно конвейерно, което означава, че оценката
на времето за изпълнение на голям брой задачи (n на брой) ще бъде дадена със следната формула
![]()
Съпоставяме
оценките (4.5.5) и (4.5.15) като образуваме отношението
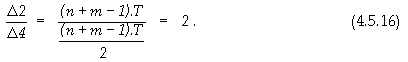
Полученият резултат позволява извода, че
производителността на асинхронния конвейер ще бъде най-вероятно най-малко два
пъти по-висока в сравнение с тази на синхронния. В отделни времеви интервали
производителността може да бъде значително по-голяма.
Заключение
В резултат на това изследване са получени количествени
оценки за производителността на различни по вид организации на изчислителен
процес. Това позволява да бъдат направени качествени сравнения. Освен това тези
оценки позволяват да бъде даден отговор на естествено възникващия въпрос
“колко?”, когато се представя нова разработка, тъй като сравнението с познатите
резултати е неизбежно. Така например, постановката, описана в случай 1, може да
се възприема като аналог на класически Фон’Нойманов процесор, т.е. като
еднопроцесорен изчислител с програмно управление. По същата логика случай 4
може да се възприема като асинхронен m-степенен
конвейерно организиран изчислител. При съпоставяне на тези два вида
изчислители, прилагайки горе получените оценки,
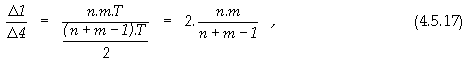
където, аналогично на (4.5.8), за множителя в горната формула се получава
същия резултат. Така можем да твърдим, че производителността на четвъртия по
вид изчислител е най-малко 2.m пъти по-висока в сравнение с първия.
Обобщеното сравнение е представено с таблица 4.5.1.
Таблица 4.5.1.
Сравнителни оценки за производителност спрямо базовата Р1
|
№ |
Вид на организацията и метод на управление |
Произво- дителност |
|
1 |
Последователно
(не конвейерно) синхронно управление на изпълнението на n
на брой задачи |
P1 |
|
2 |
Паралелно
(конвейерно) синхронно управление на изпълнението на n на брой задачи |
m.P1 |
|
3 |
Последователно
(не конвейерно) асинхронно управление на изпълнението на n на брой задачи |
2.P1 |
|
4 |
Паралелно
(конвейерно) асинхронно управление на изпълнението на n на брой задачи |
2.m.P1 |
4.6.
Закон за разпределение на закъснението при събиране
При реализация на операцията сумиране възникват преноси.
В редица случаи те образуват последователности (верижки от единици). От
дължината на тези верижки зависи латентността на комбинационния суматор.
Латентността или още закъснението, с което се получава даден резултат, е
същността на асинхронното управление. Тъй като закъснението е случайна
величина, представлява интерес изучаването на нейното поведение като такава.
Познавайки това поведение, ще можем да направим съответните изводи за целия
изчислителен процес.
Изследването се нуждае от определяне на закона на
разпределение на закъснението при сумиране на две произволно зададени числа. За
това математическата статистика изисква наличието на реални оценки и натрупване
на достатъчно големи по обем извадки от такива оценки.
За целите на експеримента е организирано числено
генериране на двойки случайни 32 битови цели числа. С помощта на специално
създадена програма е определена максималната дължина на верижката от
последователни преноси при събиране всяка двойка числа. Така изчислените
закъснения при операция събиране са натрупани в три отделни извадки с обем
1000, 3000 и 5000 числа.
Определянето на закона на
разпределение на разглежданата случайна величина, означена w –
максимална дължина на верижката от последователно разпространяващи се преноси,
е проведено най напред аналитично, с прилагане на широко известните дискретни
разпределения. За съжаление това изследване даде отрицателен резултат. В
последствие беше възприет експериментално-статистически подход: обоснован избор
на предварително зададена структура на закона на разпределение, определяне на
неговите параметри и проверка на адекватност с прилагане на статистически
критерий.
Първоначално са определени
максималните и минимални стойности на w, оценките на
централните моменти на извадките, характеризиращи дисперсията (m2),
асиметрията (m3) и ексцеса (m4). На тяхна
база са определени стойностите на следните величини
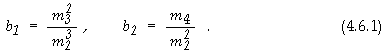
Стойностите на
тези величини за трите извадки са дадени в следващата таблица.
Таблица 4.6.1.
|
Обем на извадката |
m2 |
m3 |
m4 |
b1 |
b2 |
Max(w) |
Min(w) |
|
|
|
1000 |
12,3524 |
47,2011 |
684,00 |
1,1827 |
4,4843 |
25 |
1 |
1,78 |
22,4 |
|
3000 |
12,9314 |
60,4722 |
949,0705 |
1,6911 |
5,6756 |
29 |
1 |
1,31 |
27,6 |
|
5000 |
12,4722 |
55,5309 |
832,6225 |
1,5894 |
5,3526 |
28 |
0 |
13,73 |
30,1 |
От анализа на таблицата се вижда, че разпределението има
положителна асиметрия и значителни стойности на ексцеса. Освен това
разглежданата случайна величина е ограничена отдолу, т.е. с нулева дължина на
верижките. На тази основа е избрано разпределение на Джонсън със следната
опростена структура, съответстваща на логаритмично нормално разпределение
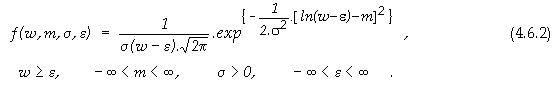
След определяне на параметрите на това
разпределение, за проверка на съгласуваността на тази функция с
експерименталните данни, е издигната нулева хипотеза Н0 за адекватно статистическо представяне на
същите. За проверка се използва критерия на
Χ2 (на Пирсон).

където
означенията са:
i -
номер на интервала;
N
- обем на статистическата извадка;
ni - брой попадения
в i-тия интервал;
fi - честота на
попадения по теоретичния закон.
Изчислената стойност на този критерий по (4.6.3) и
табличната му стойност, определена по
ν=max(w)-r-2-1
степени на свобода, са дадени в последните две колони на таблица 4.6.1. В
израза за ν, означението
r отчита обединените интервали, съдържащи
по-малко от 9 попадения.
Тъй като
![]()
то с вероятност над 95% може да се приеме, че
разпределението на експерименталните данни не противоречи на издигнатата хипотеза Н0 , т.е. разпределението на
действителните закъснения на суматора, е логаритмично нормално.
Забележка: При обработка в средата на MATLAB на
извадката с обем N=5000, се появи единичен интервал с нула броя попадения,
което създава трудности при логаритмуване. Ето защо е приета стойност 0,0001.
На фигурите по-долу са представени
хистограмите на честотата на попадение
ni (вляво) и nfi=N.fi (вдясно), в съответните интервали
с дължина единица, а под тях съответните вероятности pi (вляво) и
теоретичното разпределение fi (вдясно), за извадката с обем N=1000.
Фиг. 4.6.1. Честота
на попадение – според данните и според теоретичния закон (N=1000)
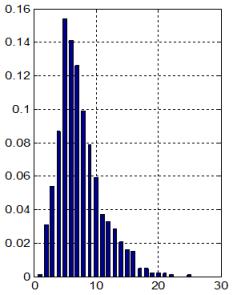
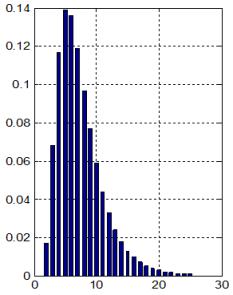
Фиг. 4.6.2. Разпределение
на вероятностите pi и на теоретичното разпределение fi
На фигурите по-долу са представени
хистограмите на честотата на попадение
ni (вляво) и nfi=N.fi (вдясно), в съответните интервали
с дължина единица, а под тях съответните вероятности pi (вляво) и
теоретичното разпределение fi (вдясно), за извадката с обем N=3000.
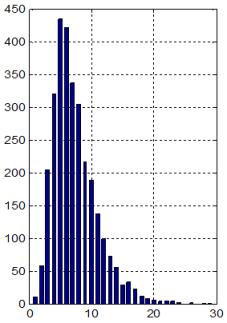
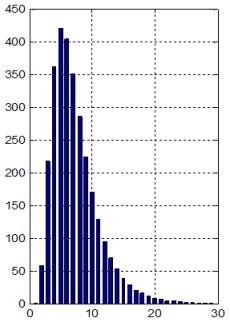
Фиг. 4.6.3. Честота
на попадение – според данните и според теоретичния закон (N=3000)
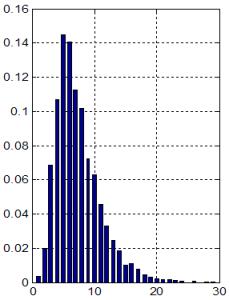
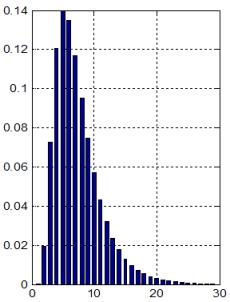
Фиг. 4.6.4. Разпределение
на вероятностите pi и на теоретичното разпределение fi
На фигурите по-долу са представени
хистограмите на честотата на попадение
ni (вляво) и nfi=N.fi (вдясно), в съответните интервали
с дължина единица, а под тях съответните вероятности pi (вляво) и
теоретичното разпределение fi (вдясно), за извадката с обем N=5000.
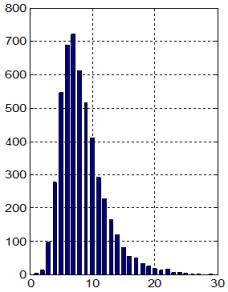
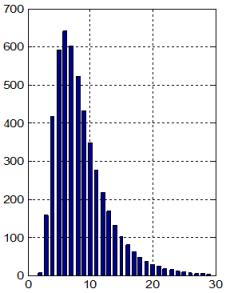
Фиг. 4.6.5. Честота
на попадение – според данните и според теоретичния закон (N=5000)
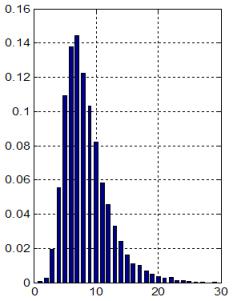
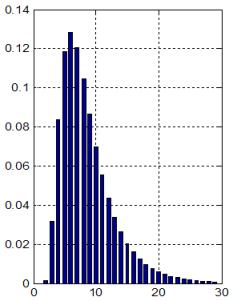
Фиг. 4.6.6. Разпределение
на вероятностите pi и на теоретичното разпределение fi
В таблица 4.6.2 са дадени параметрите на модела, получени
по трите извадки от данни
Таблица 4.6.2
|
N |
|
|
|
|
1000 |
1,9 |
0,477 |
0 |
|
3000 |
1,8872 |
0,483 |
0 |
|
5000 |
1,8938 |
0,5428 |
0 |
Заключение
Тъй като диапазона на хистограмите е с приетата дължина
на разрядната мрежа (32[b], без 1 бит за знак), то дори с просто око се вижда,
че най-вероятната дължина на верижките от последователно разпространяващи се
преноси в действителност, е почти два пъти по-къса в сравнение с приетата
(според нормалния закон на разпределение) в предходния раздел. Крайният извод,
който може да се направи е, че производителността на асинхронния конвейер е
поне 2 пъти по-висока от посочената в таблица 4.5.1.
4.7.
Мулти-формен, мулти-форматен цифров компаратор
Въведение
Операция сравнение Compare(x,y), на две числа x
и y е често срещана в алгоритмите. За изпълнение на тази операция в
системата от машинни команди на всеки цифров процесор се включват съответни
машинни команди CMP. Операнди x и y на тези команди са
числа със знак и могат да бъдат представени в различни форми (ФЗ или ПЗ).
Установяването на отношението между двете числа
![]()
цели да формира и
присвои съответните истинни стойности на признаците LT (Less Than), EQ
(equal) и GT (Greater Than) според следните правила:
![]()
![]()
![]()
Операция сравнение се изпълнява в АЛУ на цифровия
процесор чрез привеждане на отношението (4.7.1) към еквивалентното му, след представяне
на операндите в инверсен машинен код (обратен или допълнителен)
![]()
Като се отчете още, че числата могат да бъдат представени
в различни бройни системи, в различни машинни кодове, а така също и в различни
форми и формати, с голяма увереност може да се твърди, че такова изпълнение на
операция сравнение е възможно най-бавното.
В същото време съществуват хардуерни структури, които
съдържат в себе си като логически възли комбинационни компаратори, както и
съществуват интегрални схеми, съдържащи единствено цифрови компаратори,
позволяващи каскадно удължаване на разрядността на числата. В тези случаи
комбинационният компаратор е синтезиран въз основа на алгоритъма за без знаково
сравнение на две двоични комбинации, при което основното му достойнство е
високото бързодействие.
Описаното тук изследване е посветено на един принципно
нов подход за изграждане на многофункционални цифрови компаратори, способни на
високоскоростно изпълнение на операция сравнение, чрез хардуерна реализация на
операция (4.7.1). Многофункционалността се изразява в заложената мултиформеност
и мултиформатност, позволяваща сравнението на:
1. Цели и дробни двоични
числа без знак, както и такива със знак, представени в прав, в обратен или в
допълнителен кодове, както и в техните модификации;
2. Цели и дробни
двоично-десетични числа без знак, както и такива със знак, кодирани в код 8421,
8421+3, 4221, 2421, представени в прав, в обратен или в допълнителен
кодове, както и в техните модификации;
3. Числа, представени във
форма с плаваща запетая според стандарта IEEE-754.
Възможностите на такава логическа схема я определят като
универсална или още като инвариантна към фόрмата и формата за представяне
на сравняваните числа.
4.7.1. Основни съображения относно представянето на
числата
Какъвто и да е видът на представените числа, всеки от
горните случаи се разпада на 4 подслучая, в зависимост от знаците им.
Практически това е единственото общо нещо между изброените по-горе 3 случая.
Налага се изводът, че независимо от всички останали характеристики, основавайки
се на алгебрическия смисъл на числата, сравнението на знаците еднозначно
определя стойностите на признаците (2), (3) и (4), когато те са различни както
следва
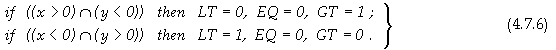
Техническата реализация на сравнението на знаковите
битове е облекчено от факта, че във всички форми, в които се представят
числата, знаковият бит е най-левият (най-старшият) в разрядната мрежа. Веднага
следва да се отбележи, че в резултат на избраната кодировка за знака на числата
(0 за положителни и 1 за отрицателни), алгоритъмът на без знаковото сравнение,
при сравнение на знаковите битове, ще определя признаците (4.7.6) на отношение
(4.7.1) неправилно, т.е. инверсно, възприемайки знаковия бит по стойност, а не
по смисъл.
В случаите, когато знаците на числата са еднакви,
алгоритъмът на без знаковото сравнение ще определя признаците (4.7.2), (4.7.3)
и (4.7.4) след сравнение на останалите битове на комбинациите, представящи
числата. Това налага разглеждането на случаите по отделно, тъй като останалите
битове са функция на машинния код.
Изказаните по-горе съображения обаче не са в сила за без
знаковите числа, тъй като при тях старшият бит трябва да се възприема по
стойност. Това налага предварително инициализиране на този случай, тъй като е
изключение от го горните правила.
А) Двоични
числа
Когато числата имат знак, за тяхното машинно
представяне се използва обратен или допълнителен код, за получаването на които
е необходим прав код. За n-битова разрядна мрежа с дясно фиксирана
запетая тези кодове се дефинират така (вижте книга [1] и книга [2]).
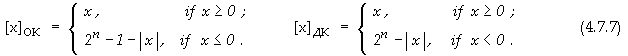
където чрез n е означена дължината на мултиформатната разрядна мрежа.
Различните формати са възможни благодарение на правилото за знаково разширение
на числата. Аналогична зависимост дефинира инверсните кодове и за двоичните
числа с ляво фиксирана запетая.
В първия случай на (4.7.7), когато и двете
числа са положителни, отношението на двата инверсни кода
![]()
е еквивалентно на отношение (4.7.1) и може да се изчисли
чрез алгоритъма на без знаковото сравнение.
Във втория случай на (4.7.7), когато и двете
цели числа са отрицателни, отношението на двата инверсни кода се изразява
съответно чрез отношението на числата
![]()
което очевидно също е еквивалентно на (4.7.1) и за двата
кода, тъй като по-малкият модул ще генерира по-голяма по стойност разлика.
Налага се обобщението, че алгоритъмът на без
знаковото сравнение може да се използва за сравняване както на числа без знак,
така и на числа със знак, представени в инверсни машинни кодове, включително и
модифицирани такива, които имат по 2 знакови бита. Това важи и за числата с
ляво фиксирана запетая, както и за числата, структурирани с цяла и дробна част.
С други думи положението на запетаята е без значение, тъй като тук се имат
предвид само числа, представени в позиционни бройни системи.
Когато сравняваните числа са представени в
прав или в обратен код, се налага предварително автоматично разпознаване и
игнориране на знаковите нули (+0, -0), едно различие, което има място в тези
два кода. Това лесно може да бъде осигурено с хардуерни средства.
Специален коментар заслужава сравнението на
числа представени в прав код, който за цели числа се дефинира както следва
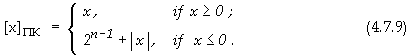
В първия
случай на (4.7.9), когато и двете числа са положителни, отношението на двата
кода
![]()
е еквивалентно на отношение (4.7.1) и може да се изчисли
чрез алгоритъма на без знаковото сравнение, тъй като то всъщност представлява
отношението
![]()
Във
втория случай на (4.7.9), когато и двете цели числа са отрицателни, отношението
на двата кода се изразява съответно чрез отношението на числата
![]()
което очевидно се решава чрез отношението
![]()
В резултат на това признаците се определят вярно, само
когато модулите са равни. При различни модули в този случай, стойностите на
признаците LT и GT, се определят неправилно – техните правилни
стойности са инверсни. Изключенията, което генерират числата със знак обаче
могат да бъдат дешифрирани и всички възможни случаи да бъдат обобщени от
следната логическа функция
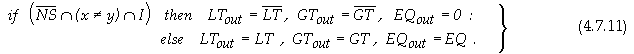
където с I
(inversion) е означена логическата функция
![]()
а с индекс out са означени крайните изходни за
компаратора стойности на признаците.
Както се вижда от (4.7.11) и (4.7.12), за идентификация
на всички изключения, логическата схема на компаратора е функция от два
допълнителни сигнала:
1. Сигнал NS (Not Signed numbers), деклариращ, че числата са без
знак;
2. Сигнал RC (Right Code - Integer binary numbers in signed magnitude
form), деклариращ, че числата са представени в прав код.
Б) Двоично-десетични
числа
Десетичните числа се представят като наредена
последователност от кодовите комбинации на своите десетични цифри. Десетичните
кодове представихме в предходните глави на тази книга. Такива кодове са (8421),
(8421+3), (2421) и др. Най-широко се прилага първият
от посочените. Машинните кодове на цели числа със знак се дефинират така
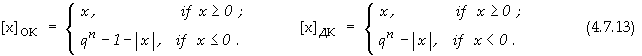
където с q е означена основата на бройната система, в която е
представено числото, като в частност тук се има предвид q=10. С n отново
е изразена дължината на мултиформатната разрядна мрежа. За всеки 2/10-чен код е
известна (книга [1] и
книга [2])
алгоритмична схема за постигане на зависимостта (4.7.13), която изхожда от
техния прав код. Както и за двоичните числа, знаковите нули в прав или в
обратен код следва предварително да бъдат дешифрирани и уеднаквени.
Прилагането на алгоритъма на без знаково
сравнение за проверка на отношението
![]()
на 2/10-чни числа напълно съответства на зависимостите
(4.7.2), (4.7.3), (4.7.4) и (4.7.6). При изпълнение на този циклически
алгоритъм, на сравнение се подлагат две цифри в текущия i-ти десетичен
разряд dxi*dyi. Тъй като тези
цифри са представени с двоични комбинации, това отношение се проверява бит по
бит по силата на алгоритъма на двоичното без знаково сравнение. От това следва,
че отношението за тези две цифри ще бъде вярно, ако за техния 2/10-чен код е в
сила свойството монотонност. Това свойство е в сила и за кодовите комбинации на
десетичните цифри в инверсни машинни кодове на числата със знак. От тук следва
окончателният извод, че алгоритъма на двоичното без знаково сравнение може да се
приложи и върху различно кодирани 2/10-чни числа. Алгоритъмът е инвариантен към
положението на запетаята на числата.
Правият код на 2/10-чните числа се дефинира
както следва
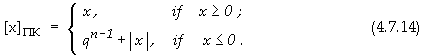
Всичко казано преди това за сравнението на
двоичните числа в прав код, е в сила и за 2/10-чните числа в прав код. Ето защо
логическата функция (4.7.11) е в сила и за тези числа. Следва, че тя е
инвариантна към основата на бройната система, в която са представени числата.
В) Числа
във форма с плаваща запетая
Разглежда се структура на разрядната мрежа според
стандарта IEEE-754 с техника на скрития бит, имаща вида, представен на фигура
4.7.1.
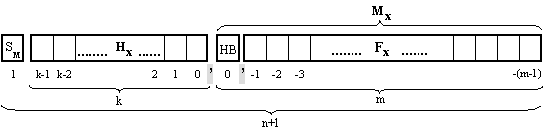
Фиг. 4.7.1. Структура на разрядната мрежа
в която
означенията са:
SM –
знаков бит на мантисата (на числото);
HX –
характеристика.
За характеристиката са в сила следните зависимости:
![]()
HB – скрит бит;
MX –
нормализирана мантиса. Има вида:
MX = 1,FX ;
FX –
фракция.
Мултиформатността се осигурява от променящите се дължини k (8, 11 или 15 бита) и m (23, 52 или 64
бита), дефинирани от стандарта.
Мантисата е число със знак и се представя в прав код.
Това означава, че отношението (4.7.1) може да бъде определено чрез алгоритъма
на без знаковото сравняване. Това отношение обаче следва да бъде съобразено с
характеристиките на числата. Характеристиките се възприемат като числа без знак
и по стойност също могат да се сравнят чрез алгоритъма на без знаковото
сравняване. Тяхното отношение обаче трябва да се приложи върху стойностите на
порядъците, които са числа със знак.
Според (4.7.15) отношението
![]()
се разглежда във
вида
![]()
който може да бъде
сведен до
![]()
Последното отношение обаче не винаги е еквивалентно на
отношението на характеристиките, тъй като порядъците са числа със знак, а те
могат да се случват в 4 различни комбинации.
Комбинациите от различни знаци съответстват на правилно
определено чрез сравняване на характеристиките отношение, тъй като отрицателният
порядък води до операция изваждане (виж (4.7.15)), което силно отдалечава по
стойност съответната характеристика от другата. В случай, че знаците са
положителни, отношението на характеристиките е в пълно съответствие с отношение
(4.7.17). В последния случай, когато знаците на порядъците са отрицателни, в
резултат на операция изваждане, отношение (4.7.17) също в съответствие с
отношение (4.7.16). В случай на две отрицателни числа, по-голямо е числото с
по-малкия порядък.
Сравнението на мантисите, като числа със знак,
представени в прав код, напълно съответства на казаното вече за числата с
фиксирана запетая. Тъй като при тези условия сравнението генерира същите
изключения, следва да се приложи логиката на функция (4.7.11).
4.7.2. Логическа схема на компаратора
Логическата схема на компаратора е синтезирана в
съответствие с алгоритъма за без знаковото сравнение и представлява
последователност от еднобитови компаратори. Тя е синтезирана според следната
логика
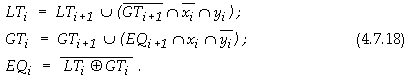
Принципната логическа схема за всички средни i-ти
разряди (i=(n-2), (n-3), … ,2, 1) е представена на фигура 4.7.2.
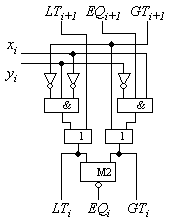
Фиг. 4.7.2. Логическа схема на i-тия бит
Логическата схема на компаратора в най-старшия (n-1)-ви
разряд (фигура 4.7.3) е синтезирана като функция и от инициализиращите сигнали NS
и RC. По този начин, когато числата генерират описаните изключения и
изходните признаци трябва да се инвертират, в този разряд се генерира
разрешението E
(Enable), което се използва в най-младшия (нулевия) разряд на
компаратора. Логиката на схемата е следната
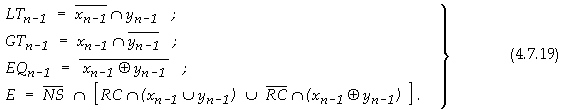
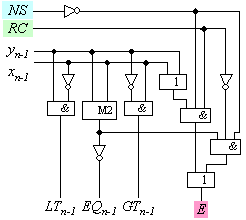
Фиг. 4.7.3. Логическа схема на старшия бит
Изключенията, които генерират числата със знак в прав и в
допълнителен код, могат да бъдат игнорирани, ако знаковите битове на числата
бъдат инвертирани преди сравнение. С други думи, предварителната инверсия на
знаковите битове заменя смисъла на кодовите цифри на знаците с числена
стойност, водеща до правилно определяне на признаците. Така при сравнение на числа,
представени в инверсни машинни кодове, не се генерират изключения. Изключение
се генерира единствено при две отрицателни числа, представени в прав код.
Логиката за дешифриране на това изключение е представена от функция (4.7.11), в
която обаче следва да се използва следната логическа функция
![]()
Логическата схема на компаратора в най-старшия (n-1)-ви
разряд (фигура 4.7.4) е синтезирана аналогично, но при отчитане на зависимостта
(4.7.20) за инициализиращия сигнал I.
Логиката на схемата в този втори вариант е следната
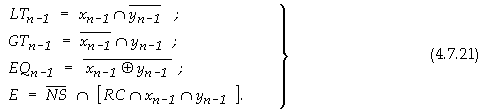
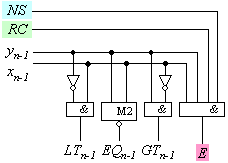
Фиг. 4.7.4. Логическа схема на старшия бит
(с предварителна инверсия на знака)
Очевиден е изводът, че апаратната реализация на (4.7.21)
е по-икономична в сравнение с тази на (4.7.19).
Логическата схема на компаратора в най-младшия 0-лев разряд е представена на фигура 4.7.5. Както се вижда, изходните
стойности на признаците са функция от разрешението Е, чиято логика е
следната
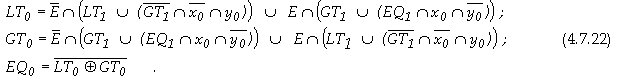
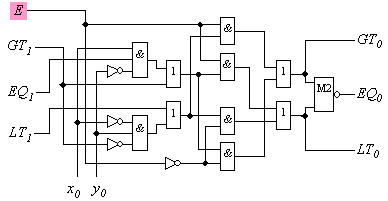
Фиг. 4.7.5. Логическа схема на младшия бит
Разрешението влияе на окончателните резултати само в
случай, че числата са във форма с плаваща запетая и са отрицателни и не са
напълно еднакви.
4.7.3. Числени
примери за сравнение
ПРИМЕР 1.
Да се сравнят числата x=-16
и y=-19 представени в допълнителен код във формат 8
бита. Отговорът е GT=1.
![]()
![]()
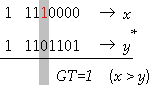
Както се вижда от примера, знаците на числата
са еднакви и отношението се определя правилно от цифрите в цифровата част.
Сравнението на правите кодове на същите две
числа
![]()
![]()
води до следния резултат
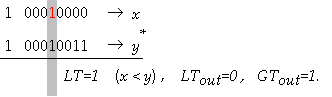
Както се вижда от примера, сравнението определя
неправилен отговор (x<y). Този отговор е поправен след съответната инверсия,
в съответствие с работата на синтезирана логическа схема и изходните признаци LТout
и GТout са правилни.
ПРИМЕР 2.
Да се сравнят 2/10-чните 5 цифрени числа
x=-6170 и y=-3369 , представени в код 8421 и в допълнителен код. Отговорът е
LT=1.
![]()
![]()
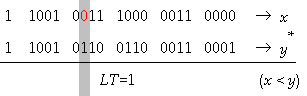
Както се вижда от примера, знаците на числата
са еднакви и отношението се определя правилно от цифрите в цифровата част.
Сравнението на правите кодове на същите две
числа
![]()
![]()
води до следния резултат
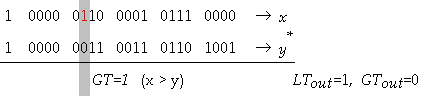
Както се вижда от примера, сравнението
определя неправилен отговор (x>y). Този отговор е поправен след съответната
инверсия, в съответствие с работата на синтезирана логическа схема и изходните
признаци LТout и GТout са правилни.
ПРИМЕР 3. Да се сравнят две числа,
представени във форма с плаваща запетая, във формата от фигура 4.7.1.
Пример 3.1. Да се сравнят числата
![]()
Резултатът от това сравнение се получава
лесно и бързо, тъй като завършва още при сравнение на знаците на числата: x>0, y<0,
следователно GT=1.
Пример 3.2. Да се сравнят числата
![]()
Резултатът и от това сравнение се получава
лесно и бързо, тъй като завършва още при сравнение на знаците на числата: x<0, y>0,
следователно LT=1.
Пример 3.3. Да се сравнят числата
![]()
Резултатът от това сравнение не може да се
получи лесно и бързо, тъй като знаците на двете числа са еднакви. Така след
сравнение на знаковите битове, в посока надясно, алгоритъма продължава със
старшия бит на характеристиката.
Тъй като порядъкът px<0, то старшият бит на характеристиката Hx ще съдържа нула, т.е. Hx[k-1]=0. В същото време py>0. Това
означава, че старшият бит на характеристиката
Hy ще съдържа
единица, т.е. Hy[k-1]=0. В резултат от сравнението на старшите битове
на характеристиките за отношението на числата ще бъде определен признак LT=1, т.е.
0,00005 < 600.
Пример 3.4. Да се сравнят числата
![]()
В този случай знаците на числата са отново
еднакви и характеристиките са същите. Сравнявайки ги отново ще се получи същия
признак LT=1, което за характеристиките е вярно, но за числата като цяло
не е вярно, тъй като отчитайки знаците им, отношението е: -0,00005 > -600. В този случай правилните стойности на признаците
LT и GT са инверсните, т.е. правилният отговор е LТout=0 и GТout=1.
Изключението, което се изявява в работата на
компаратора в този случай, се дължи на факта, че мантисите на числата са
представени в прав код. Това неизбежно изисква предварителна инициализация на
логическата схема. Тази инициализация може да бъде реализирана с вече
предложения сигнал RC. Стойностите на изходните признаци се определят от
функция (4.7.9).
Заключение
Синтезът на цифров компаратор с множеството различни
характеристики се оказа възможен. Синтезираната логическа схема прилага
последователно сравнение, но може да бъде преструктурирана като пирамидална.
Схемата е мултиформена, защото е инвариантна към
запетаята на числа, представени в позиционни бройни системи. Тя е инвариантна
още към различните машинни кодове (прав, обратен, допълнителен и техните модификации).
Схемата е мултиформатна, тъй като е инвариантна към
дължината на разрядната мрежа, в която са представени числата, което се дължи
на свойствата на инверсните машинни кодове.
Схемата е инвариантна още към кода за представяне на
десетичните цифри, стига той да притежава свойството монотонност, което е
показано тук за няколко от най-прилаганите.
Схемата проявява своите универсални възможности и върху
числа представени във форма с плаваща запетая според стандарта IEEE-754.
Доказано е, че синтезираната схема успешно се справя в три от четирите случая
на комбиниране на знаците на такива числа. Изключението, което може да се яви
при числа с отрицателни знаци, успешно се дешифрира, при това с минимални
апаратни средства, не влияещи на латентността й. Синтезирани са два различни
варианта за корекция на признаците. Мултиформатността на схемата е в сила и
върху числата с плаваща запетая благодарение на адитивната функционалност,
според която е дефинирана характеристиката на числата.
Времето за превключване на цифровия компаратор е функция
от самите числа, ето защо то е променлива величина,
която има случаен характер и геометрично разпределение. Статистическите
резултати налагат обобщението, че в рамките на допустимото ниво на значимост за
критерия на Пирсон, очакваното време за превключване на компаратора е в
границите на 1/3 от неговата дължина, т.е. около 10[b] от дължината на
разрядната мрежа.
4.8.
Закон за разпределение на закъснението при сравнение
Следващата операционна схема, която се
характеризира със променливо и значително закъснение е цифровия компаратор.
Времето за превключване на логическата схема на компаратора е основен
технически параметър, който го характеризира. Той е необходим при управлението
на операция сравнение в условията на асинхронно управление. В случая, времето
за превключване е пропорционално на дължината на верижката, образувана от
срещнатите в посока към младшите разряди последователно еднаквите старши цифри
в двете числа. При среща на различни цифри в текущия бит, признаците се определят
еднозначно и останалите до най-младшия бит цифри, не се нуждаят от сравнение.
Така, разглеждана като случайна величина, времето за превключване на
логическата схема, т.е. на латентността й, се нуждае от специално изследване.
За целта беше организиран и проведен числен експеримент чрез програмен модел на
компаратора. В модела на сравнение са подлагани двойки числа, генерирани като
псевдослучайни. Сравняваните числа са генерирани в 32-битовия диапазон на
разрядната мрежа, като получените дължини за латентността на компаратора при
всяко сравнение, са натрупани в извадки с обем 1000 и 5000 сравнения.
Статистическото изследване на получените
извадки има за цел да намери закона за разпределение на случайната величина,
както и неговите параметри. Последните са необходими за оценка на
производителността на компаратора, когато е използван в други изчислителни
структури и както вече отбелязахме, в условия на асинхронно упраление.
Като модел на верижката от фактически
извършени сравнения с резултат равно (EQ) се използва величината (w-1),
където с w е
означен номерът на съответния бит. Всеки бит, в който очакването да бъде
прекратена верижката от последователни съвпадения не се реализира, се оценява с
вероятност (1-p). Тогава вероятността, верижката да не бъде прекъсната
след (w-1)-тия бит, е равна на (1-p)(w-1).
С отчитане на условието, че в бит w събитието прекъсване ще се състои с вероятност [1-(1-p)]=p, то законът за разпределение се приема да има
вида:
![]()
Видът на тази функция дава основание да бъде
издигната нулева хипотеза Н0 за статистическата апроксимация на
латентността на компаратора със закона за геометрично разпределение. За
определяне на параметъра р в (4.8.1) и неговата адекватност към
експерименталните данни е използван критерия на Пирсон:

където: i -
е номер на интервала;
N - обем на статистическата извадка;
ni - брой попадения
в i-тия интервал. Случайната величина w има 32 възможни стойности, които могат да се
разпределят в 31 интервала на 32 битовата разрядна мрежа;
fi - честота на
попадения по теоретичния закон.
За проверка на достоверността на числените
оценки, за двете последователности от сравнявани числа е изчислен коефициента
на взаимна корелация r.
За случая от 1000 сравнения е получена стойността r1000=0,0042, показваща с голяма достоверност
взаимна независимост между двете сравнявани последователности. Числените резултати от проведеното статистическо изследване,
получени в средата MATLAB, са представени в таблицa 4.8.1, в която са използвани
следните означения:
w - номер на
интервала, съответстващ на номера на изходящия бит на
верижката;
pi -
относителна честота на попаденията в i-тия интервал;
fni -
брой попадения, определени по теоретичния закон.
Таблица 4.8.1. За
извадка с обем 1000 сравнения
|
w |
ni |
pi=ni/1000 |
fi |
fni |
|
1 |
473 |
0,473 |
0,493 |
493 |
|
2 |
260 |
0,260 |
0,25 |
250 |
|
3 |
142 |
0,142 |
0,1267 |
127 |
|
4 |
75 |
0,075 |
0,0642 |
64 |
|
5 |
28 |
0,028 |
0,0326 |
33 |
|
6 |
22 |
0,022 |
0,0165 |
17 |
За всяка извадка са определени максималната и минимална
стойност на случайната величина, математическото очакване М, както и
нейната дисперсия S2.
В първата извадка максималната дължина на латентността е
13 бита, а минималната 1 бит. Математическото очакване има стойност М=2,035,
а дисперсията – S2=2,0658.
Вероятността, събитието да се състои, е p=0,493. Числената стойност на
критерия
![]()
е по-малка от теоретичната
![]()
определена при ниво на значимост v=0,05 и степени
на свобода k=max(w)-1=5, откъдето следва, че представените данни не противоречат на хипотезата за
геометрично разпределение.
На фигура 4.8.1 са представени хистограмите на
относителните честоти на попадение pi (вляво)
и на теоретичното разпределение f (вдясно).
Фиг. 4.8.1. Разпределение
на латентността в извадка с обем 1000 сравнения
За случая от 5000 сравнения, за коефициента
на корелация между двете генерирани последователности от числа, е получена
стойността r5000=0,0167. Тук отново с голяма достоверност съществува
взаимна независимост между двете сравнявани последователности. Във втората извадка максималната дължина на латентността
е 17 бита, а минималната 1 бит. Математическото очакване има стойност М=1,9998, а дисперсията S2=1,9918.
Вероятността, събитието да се състои, е p=0,5004.
Числената стойност на критерия
![]()
е по-малка от теоретичната
![]()
определена при ниво на значимост v=0,05 и степени на свобода k=max(w)-1=8, откъдето следва, че представените данни не противоречат на хипотезата за
геометрично разпределение.
Таблица
4.8.2. За извадка с обем 5000
сравнения
|
w |
ni |
pi=ni/1000 |
fi |
fni |
|
1 |
2467 |
0,4934 |
0,5004 |
2502 |
|
2 |
1296 |
0,2592 |
0,25 |
1250 |
|
3 |
635 |
0,127 |
0,1249 |
624 |
|
4 |
290 |
0,058 |
0,0624 |
312 |
|
5 |
162 |
0,0324 |
0,0312 |
156 |
|
6 |
64 |
0,0128 |
0,0156 |
78 |
|
7 |
47 |
0,0094 |
0,0078 |
39 |
|
8 |
20 |
0,004 |
0,0039 |
19 |
|
9 |
19 |
0,0038 |
0,0019 |
10 |
На фигура 4.8.2 са представени хистограмите на честотата
на попадение pi (вляво) и теоретичното разпределение f (вдясно).
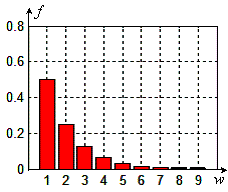
Фиг. 4.8.2. Разпределение
на латентността в извадка с обем 5000 сравнения
Заключение
Синтезът на цифров компаратор с множеството различни
характеристики се оказва възможен. Синтезираната логическа схема прилага
последователно сравнение, но може да бъде преструктурирана.
Чрез входния сигнал NS схемата различава числата без знак от
числата със знак. Схемата е мултиформатна, тъй като е инвариантна към дължината
на разрядната мрежа, в която са представени числата. Това се дължи на
свойствата на машинните кодове. Схемата е мултиформена, защото е инвариантна
към запетаята на числа, когато те са представени в позиционни бройни системи.
Тя е инвариантна още към различните машинни кодове и техните модификации.
Схемата е инвариантна още към кода за представяне на десетичните цифри, стига
той да притежава свойството монотонност.
Схемата проявява своите универсални възможности и върху
числа представени във форма с плаваща запетая според стандарта IEEE-754. Както
и във форма с фиксирана запетая, за получаване на верните стойности на
признаците, се използва допълнителния инициализиращ сигнал RC. Логическите
елементи, необходими за реализация на функцията на този сигнал, увеличава
апаратните разходи нищожно. Те не влияят на латентността на схемата.
Мултиформатността на схемата е в сила и върху числата с плаваща запетая
благодарение на адитивната функционалност (4.7.15), според която е дефинирана
характеристиката на числата.
Времето за превключване на цифровия компаратор е функция
от самите числа, ето защо то е променлива величина,
която има случаен характер и геометрично разпределение. Статистическите
резултати налагат обобщението, че в рамките на допустимото ниво на значимост за
критерия на Пирсон, очакваното време за превключване на компаратора е в
границите на 1/3 от неговата дължина, която оценяваме на около 10 бита от
разрядната мрежа. Тези числени оценки могат да послужат за статистическа оценка
на производителността на тук предложеното микроконвейерно звено, работещо в
условията на асинхронно управление.
4.9.
Асинхронен модел на фактическото закъснение за цифров компаратор
Въведение
Въпреки, че в тази книга беше казано много за асинхронния
метод на управление, във връзка с обявената тема отново ще изтъкнем, че един от
методите, чрез който може да се повишава производителността на логическите
структури, е именно този. Преминаването от синхронни към асинхронни системи
води и до други положителни последствия, като проста и евтина реализация, висока
пропускателна способност, висока надеждност и ниска енергийна консумация (low-power).
Възможен е удобен интерфейс между синхронни и асинхронни системи, или между
синхронни системи работещи с различни тактови последователности (different
clocks). Същественото при този преход е, че се преминава към
децентрализирано управление. Този вид управление се характеризира със
самосинхронизация на елементите в изчислителната структура. В условията на
съвременна булева технология, най-елегантната самосинхронизация се реализира
чрез така наречените handshake controllers. Принципът на
“ръкостискане”, въз основа на който те се синтезират, позволява реализиране на
микроконвейерна (micro-pipeline) организация, една от
съвременните форми на паралелизъм.
Същността на синхронизацията се състои в определяне на
подходящия момент, в който следва да се появи импулс за запис W (Write)
на нови данни в регистъра фиксатор (фигура 4.9.1). В синхронните системи ролята
на синхронизатор изпълняват импулсите на тактовия сигнал.
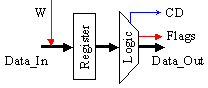
Фиг. 4.9.1. Логическа структура на звено
В асинхронните системи, където липсва тактов сигнал, при
запис на нови данни, всяко звено трябва да се самосинхронизира в зависимост от
състоянието на съседните звена (предходно и следващо). Текущото звено приема
новите данни от предходното звено в подходящия момент. Подходящият момент
настъпва, когато са изпълнени едновременно две условия – предходното звено
подава готови нови данни, а следващото звено е записало резултата от текущото
звено. С цел повишаване на производителността в асинхронните системи,
синхронизацията има за цел да определи възможно най-ранния момент за този
даннов трансфер. Това е трудна и актуална задача, защото има индивидуално
решение за различните структурни елементи, включването на които определя
алгоритъмът на изчисленията. Решаването на тази задача изисква подробен анализ на закъсненията и на състезанията (hazards)
в логическите схеми. Неотчитането на реалното поведение на логическите схеми е
причина за неправилна синхронизация и изчисления с неверни данни. Тези причини
засилват своята роля в условията на асинхронно управление. Ето защо се отделя
особено внимание на модела на фактическото закъснение (completion detection)
на изчисленията в логическите схеми. Моментът, в който сравнението фактически
завършва, логическата схема следва да съобщи за това чрез сигнал CD
(фигура 4.9.1).
Практикува се още един подход за синтез на асинхронна
логика, познат като NCL-логика (NULL Convention Logic), за който беше
писано в началото на тази книга. За постигане на синхронизация в този подход
данните и управлението са интегрирани в единен логически поток.
Синхронизиращата функция в този поток е сигналът разделител (null).
Логическите сигнали се предават парафазно по два проводника (“1-true”,
“0-false”). Данните са верни само когато се появи разделителят “null”,
в което и се изразява синхронизацията. Синхронизацията се реализира чрез
ключови схеми с хистерезис, чиито изходи могат да бъдат в две състояния – “null”
и “data”. NCL-логиката дава решение на повечето от проблемите, свързани
с Булевата логика, но както авторите сами признават, нейната реализация
неимоверно повишава апаратните разходи.
Моделът на фактическото закъснение е особено подходящ за
звена, чиято микрооперационна логика има латентност, силно зависеща от входните
данни. Типичен пример за това е цифровият компаратор, който се разглежда тук.
Латентността на тази схема е променлива величина, чийто случаен характер е
специално изследван, а получените резултати са представени в предходния раздел
4.8. Цифровият компаратор, илюстриран на фигура 4.9.2, е комбинационна схема,
която сравнява две n-битови входни комбинации x и y,
чрез алгоритъма на без знаковото сравнение. Според този алгоритъм процесът
започва със сравнение на двете най-старши цифри. При равенство се преминава
последователно към по-младшите, докато в съответния разряд се срещне различие и
се формират окончателните стойности на признаците (Flags) от сравнението
![]()
Признаците LT (Less Than), EQ (Equal) и GT
(Greater Than) се дефинират както следва
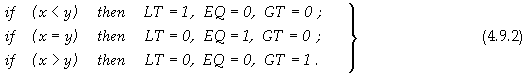
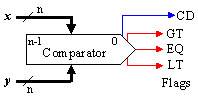
Фиг. 4.9.2. Изходи на цифров компаратор
Започвайки сравнението от старшия бит, окончателните
логически стойности на признаците (4.9.2) се формират в съответния разряд, без
значение от стойностите в останалите по-младши битове. С други думи, признаците
при различни операнди се формират с различно закъснение. Като се има предвид
търсената висока производителност чрез асинхронно управление, променливата
латентност на сравнението не е подходяща за синхронно управление. Във всеки
такт на синхронното управление, т.е. при всяко сравнение, присъства
непроизводителен времеви интервал, в който готовият резултат очаква следващия
тактов импулс. С други думи, в синхронни условия стойностите на признаците
възникват със закъснение по-малко от периода на тактовата последователност.
Тези констатации правят изследването актуално, а неговата цел е създаване на
модел на фактическото закъснение CD (Completion Detection) за цифров компаратор. Моделът е необходим за управление в асинхронни
условия (признаците LT, EQ,
GT реализират условните алгоритмични преходи в изчислителния процес).
Изложеният тук по-долу синтез на сигнала CD, се
основава на логическата схема на цифровия компаратор, представен подробно в
раздел 4.8 по-горе. За целите на синтеза тук на фигура 4.9.3 е представена
единствено логическата схема на междинните разряди.
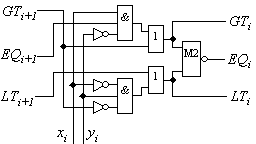
Фиг. 4.9.3. Логическа схема на текущ
(междинен) бит №(i), i=(n-2), …
3, 2, 1.
Необходимо е да се поясни, че сигналът CD се
използва от handshake контролерите като сигнал Request - заявка за даннов трансфер.
4.9.1. Модел на фактическото закъснение
След поява на нови входни данни, всяка логическа схема се
превключва. Тъй като моментът, в който превключването започва, е известен,
следва да се улови крайният момент, в който това превключване завършва.
Времевият интервал между двата момента представлява фактическото закъснение, с
което на изхода на схемата се установява окончателния резултат. Сигналът CD
трябва да идентифицира началото и края на всяко превключване на схемата, за
която е синтезиран. По време на изчисленията стойността на този сигнал определя
състоянието на схемата като заета (busy).
Основната идея в модела на фактическото закъснение се
изразява от логическата функция на паралелната парафазна (dual-rail)
дизюнкция на логически сигнал s
![]()
Практическият ефект от дизюнкцията на двете фази strue
и
sfalse при превключване на сигнала s е илюстриран графично
на фигура 4.9.4.
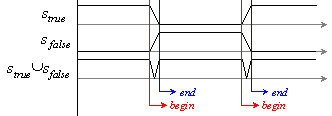
Фиг. 4.9.4. Парафазна дизюнкция на сигнали
с паралелни фронтове
Временното смущение в константния сигнал (strue
È sfalse)=1 може да се появи на практика само при
паралелни във времето фронтове в превключването на сигнал s. Времевия интервал на
смущението в логическата единица се възприема като интервал, в който
логическата схема изчислява новата изходна стойност. Изчислението се счита за
завършило с изчезване на това смущение.
Този модел за реализация на фактическо закъснение обаче
търпи сериозна критика. Той е само теоретичен и не e особено надежден на
практика, както показва и нашият опит. Основният му недостатък се дължи преди
всичко на факта, че на практика е невъзможно да се осигури абсолютната
паралелност във времето на фронтовете в двете фази strue и sfalse
при превключване на сигнала s. Отговорността за това е на технологиите, които не са в
състояние да гарантират еднакво закъснение в различните вериги от
последователно превключващи се логически елементи. Нещо повече, реализацията в
чист вид на функция (4.9.3), се постига чрез двойно увеличаване на апаратните
разходи, както ясно е показано в книга [2].
Става дума за паралелно дублиране на логическите схеми, формиращи
сигналите strue и sfalse.
В същото време, съвсем преднамерено този подход се възприема от
изследователи, заради защитата от преднамерени атаки, която той може да се
осигури. Синхронизацията за валидни данни в този случай, т.е. за улавяне на
момента за приключило превключване, се реализира чрез логическата схема на
Мюлер С-елемент.
Изискването за паралелна парафазна схемна реализация на
сигналите е много тежко. Освен това при загуба на паралелност в превключванията
на сигналите strue и sfalse , което е напълно възможно, както
парафазната дизюнкция, така и С-елементът, не са в състояние да регистрират
всяко отделно превключване и са вероятни пропуски. Нещо повече, в много реални
логически схеми двете фази на един сигнал съвсем естествено възникват
последователно във времето. Типичен пример за това са двата изхода на всеки
тригер (Q, notQ). Именно такива случаи изискват споменатото дублиране на
логическите схеми. На фигура 4.9.5 са илюстрирани ситуации на последователно
превключване на двете фази на сигнала, в резултат на което функция (4.9.3) не
винаги е в състояние да формира практическото смущение.
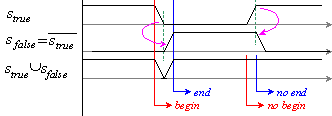
Фиг. 4.9.5. Парафазна дизюнкция на сигнали
с не паралелни фронтове
За отстраняване на посочените недостатъци и постигане на
висока надеждност за сигнал (4.9.3) тук се предлага ефективна и икономична
схема за асиметрично закъснение (asymmetric delay to the forefront)
на преден фронт. Такава схема е описана в началото на глава 5 на тази книга. В
тази схема потребителят може лесно да определя отместването във времето до
няколко фронта. Всяка от фазите на сигнал s преминава през такава схема. Дизюнкцията от
получените закъснения формира правилен и надежден отрицателен импулс с ясно
изразено ниско ниво – фигура 4.9.6.
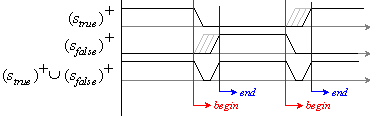
Фиг. 4.9.6. Дизюнкция на сигнали с
асиметрично закъснение на предни фронтове
Дизюнкцията от така получени сигнали с отместени предни
фронтове изпълнява при всяко превключване ролята на сигнал CD. Цифровият
компаратор, който е многоразрядна схема, формира закъснението на своето
превключване, като сума от последователните закъснения в отделните разряди. С
други думи, сигнал CD (фигура 4.9.1), трябва да се формира от
конкатенираните във времето последователни поразрядни закъснения CDi.
Това разбиране се изразява чрез следната логическа функция
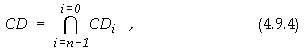
където за сигналите CDi тук се предлага практическа реализация,
основаваща се на дизюнкцията
CDi = ( strue
)+ È ( sfalse )+
(вижте фигура 4.9.6). Формираните по описания начин сигнали CDi се застъпват щафетно във времето според
(4.9.4), както е показано на фигура 4.9.7.
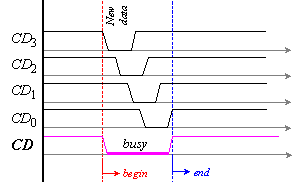
Фиг. 4.9.7. Щафетно застъпване на
сигнали CDi (4 бита)
4.9.2. Синтез на
логическа схема за фактическо закъснение на компаратор
Предвид на изказаните в раздел 2 недостатъци, свързани с
използването на двете фази на сигнала, тук се предлага нов модел на
фактическото закъснение съобразен с особеностите на цифровия компаратор. Новият
модел се основава на следното откритие в поведението на неговата схема. Тъй
като поразрядните (еднобитовите) сравнения продължават от разряд в разряд само
след равенство в текущия разряд (CDi=1), и се прекратяват след текущо
неравенство (EQi=0), то според определението (4.9.2) следва, че
сигналът EQi и дизюнкцията (LTiÈGTi) имат винаги противоположни
логически стойности. Анализирайки схемата от фигура 4.9.3, се разбира още, че
стойностите на тези признаци възникват паралелно във времето, предвид
паралелните вериги от логически елементи, които ги изчисляват. Въпреки, че в
това се открива пълна аналогия с изложената по-горе концепция за използване на
двете противоположни фази на един сигнал, тази идея тук е изоставена. За
реализация на фактическото закъснение тук се предлага следната логическа
функция
![]()
Същността на функция (4.9.5) е такава, че тя гарантира
логическа стойност нула при равенство на битовете в текущия разряд (xi=yi). Тази
стойност е стабилна и потенциална след възникването си до появата на следващите
операнди x и y на входа на компаратора. Функцията ще получи стойност единица в поредния разряд,
в който сравняваните битовете са различни. Всички следващи поразрядни функции CDi,
до най-младшия разряд, ще повторят тази стойност. Те ще възникват
последователно във времето и ще потвърждават във времето вече определените
стойности на признаците. Практически възникването на единица за поредната
дизюнкцията (LTiÈGTi) бележи във времето момента на
получаване на крайния резултат. В частния случай, когато сравняваните
комбинации са напълно еднакви, за маркиране на края на превключването на
схемата се използва стойността (EQ0=0),
възникваща последна във времето. Така за изходния сигнал CD се предлага
следната логическа функция
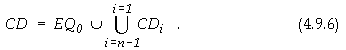
Хардуерната реализация на функция (4.9.6), представена на
фигура 4.9.8, се характеризира с изпреварващо във времето извеждане на
резултата към изхода, така щото следващите в по-младшите разряди превключвания
могат само да потвърдят (при това със закъснение) вече получения резултат.
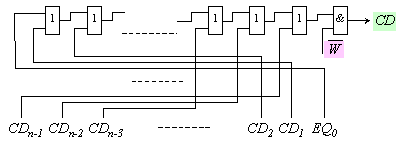
Фиг. 4.9.8. Логическа схема на сигнала CD
Включването на сигнала за запис notW към изходния
логически елемент И на схемата от фигура 4.9.8 се дължи на едно изключение.
Същността му се състои в това, че след текущо сравнение, не е изключено в
регистъра фиксатор да бъдат записани два нови операнда, със същите комбинации.
При това логическите стойности в тригерите на регистъра няма да се променят, а
само ще се потвърдят без превключване. Това означава, че в компаратора също
няма да възникнат никакви превключвания. Това ще осуети генерирането на сигнал CD.
Стробирането на изходния сигнал със сигнала за запис ще генерира краткотрайна
нула, изчезването на която може да се приеме за край на сравнението.
Процесът на превключване на логическата схема от фигура
4.9.8 и формирането на изходния сигнал, описан по-горе, е илюстриран с
конкретен пример, представен на фигура 4.9.9.
Примерът е за отношението на числата (X=-11)
и (Y=-29), представени в допълнителен код. Както е посочено, решението (X>Y)
се получава в бит №4. На времедиаграмата в пресилена форма са изразени
закъсненията на всеки отделен бит. Вижда се, че резултатите CD3,
CD2, CD1 само препотвърждават CD4.
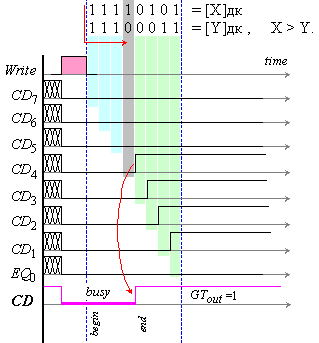
Фиг. 4.9.9. Времедиаграма на сигнала CD при
сравнение на 8-битови комбинации
Заключение
Синтезираната логическа схема (фигура 4.9.8) оценява
продължителността на логическото изчисление на признаците на отношение (4.9.1).
По време на това изчисление тя формира на своя изход логическа нула. Предният
фронт на сигнала CD маркира края на сравнението. Така поставената в
началото задача се приема за решена. Избегнато е дублирането на схеми от
компаратора и като цяло допълнителният хардуер е
минимален. Настоящото изследване е ориентирано единствено в равнището на логическото
проектиране. Не са коментирани възможностите на CAD-системите за компютърно
проектиране на ниво електронни елементи. Изложеното в началото на раздела е
достатъчно да се разбере, че срещу логическата схема на всеки еднобитов CD-модел
е противопоставен само един единствен 2-входов OR елемент (фигура 4.9.9). Това
прави решението изключително икономично в апаратно отношение. Това може
да се оцени като добър резултат, ако се има предвид, че постигането на условия
за асинхронно управление по принцип натоварва значително логическите схеми.
Хардуерната реализация на тази функция се основава на принципа за изпреварващо
във времето извеждане на резултата, чието възникване се характеризира с
променящо се местоположение по дължината на разрядната мрежа.
Този принцип може лесно да се възприеме когато се проследят логическите връзки
в схемата от фигура 4.9.8. Вижда се, че сигналът CDn-1 достига изхода CD като преминава последователно само през
2 логически елемента. В същото време сигналът CD1 следва да
превключи последователно n
на брой логически елемента. Така той закъснява и губи състезанието по отношение
на изхода CD, което е илюстрирано на фигура 4.9.9.
При всяко сравнение функцията CD генерира преден
фронт, което е необходимото условие за управление на конвейерния автомат.
Заедно с това, принципът за изпреварващо във времето извеждане на резултата към
изход, може да бъде приложен и за признаците LT и GT.
4.10.
Конвейерен умножител с концентратори
В този раздел е изследвана възможността за реализация на
конвейеризиран схемен умножител. По време на синтеза е приложен концентратор от
тип 3:1, разгледан в раздел 4.2. Показано е, че в резултат неговото приложение води до алгоритъм за умножение, който е
от класа на алгоритмите за умножение с 2 разряда едновременно. Комбинационните
схемни умножители, въпреки изключително прецизния си логически
синтез, предвид голямата дължина на операндите, имат голяма латентност в
сравнение с латентността на обикновен суматор. Това може да бъде причина за
неравномерен темп на конвейерите. Ето защо е актуална конвейерната организация
на схемния умножител. Тя е актуална още по причини, изтъкнати тук в раздел 2.1.
Синтез на конвейерния умножител
Възможната логическа структура на конвейерния
умножител се характеризира с това, че съдържа n на брой
нива или още степени за едновременно движещите се междинни суми и съответните
им двойки съмножители, представени в n-битова
разрядна мрежа. Логическа структура може да поеме конвейерното изпълнение на
множество последователни операции умножение, от които в конвейера ще се
изпълняват паралелно във времето n на брой от тях. Така на
всеки такт от конвейера ще слиза поредната двойка съмножители и съответното й
произведение. Закъснението на дадено произведение по отношение момента, в който
съмножителите се зареждат в конвейера, е равна на n такта.
Ако приемем, че едно последователно умножение на 2 числа отнема n на брой такта, то последователното изпълнение на n на брой операции умножение би отнело n2 на брой такта. Същият брой умножения, с помощта на
конвейерно организиран схемен умножител, би отнело 2.n на брой такта. Така се разбира, че конвейерната организация, в
сравнение с последователната, е в състояние да повиши производителността на
процесора при последователно изпълнение на умножение, до n/2 пъти, т.е. примерно, при 32-битова разрядна мрежа, увеличението
достига 16 пъти. Разбира се, конвейерната организация може да бъде реализирана
и асинхронно, с помощта на 2-фазови или 4-фазови конвейерни автомати. В този
случай, благодарение на фактическата латентност, производителността на
конвейерния умножител ще нарастне допълнително.
В този раздел представяме синтеза и
изследването на оригинална логическа структура на конвейерен умножител, чиято
организация се отличава от известните по това, че формира междинните суми като
паралелни суми от 3 числа, с помощта на концентратор от типа (3:1), чийто
синтез представихме в раздел 4.2.
Традиционно, при умножение
на n-битови числа без знак, междинните суми се получават както следва
![]()
![]()
За да натоварим обаче тривходовия суматор,
който приемаме да използваме като оператор на дадено ниво в конвейера, трябва
да формираме междинната сума както следва
![]()
![]()
От горния израз се вижда, че във всяка нова
междинна сума се натрупват две последователни поразрядни произведения. От тук
веднага следва изключително положителният извод, че броят на формираните с
помощта на такива суматори междинни суми, ще бъде два пъти по-малък и за
техният индекс j можем да запишем закона:
![]() .
.
За логическия синтез на суматора, който ще
реализира сумата (4.10.2), е полезно тя да бъде илюстрирана със схемата от
фигура 4.10.1.

Фиг. 4.10.1. Схема
за натрупване на поредната междинна сума
Схемата показва, че младшите разряди (на брой 2.j) в
j-тата междинна сума са окончателно получени при предходните събирания и
следователно могат да бъдат пропуснати и изключени от текущото събиране. От тук
следва, че всички концентратори, употребени в отделните нива на конвейера,
следва да бъдат с една и съща дължина и съответно изместени наляво един спрямо
друг, в съответствие с нарастващия порядък на използваните битовете от
множителя (тук се има предвид методът за умножение с младшите разряди напред).
Синтезът на принципната логическа схема на тук прилаганите концентратори се
различава от този, изложен в раздел 4.2, само по това, че трите числа са
разместени едно спрямо друго на един бит, в съответствие с формула (4.10.2).
След така изложените съображения следва, че получената
структура на конвейерния умножител, реализиращ натрупването (4.10.2), ще
съдържа два пъти по-малко на брой степени, тъй като на всяко ниво тя консумира
едновременно по два бита от множителя. Така, структурата на конвейерен
умножител с концентратори от типа (3:1) ще има вида, показан на фигура 4.10.2.
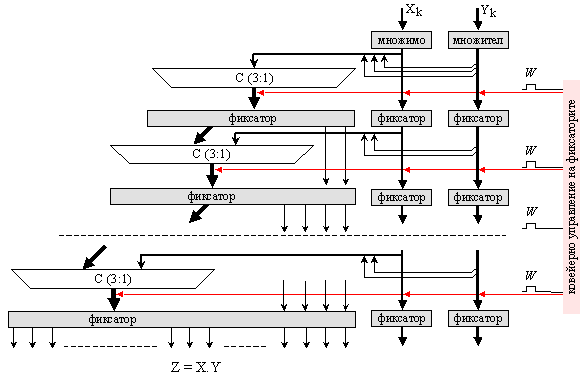
Фиг. 4.10.2. Логическа структура на конвейерния
умножител
Входните операнди са означени с индекс k, с което е показано, че
са поредната двойка в конвейерното умножение.
Както се вижда от фигура 4.10.2, първата междинна сума се
формира като сума от следните три поразрядни произведения
![]()
![]()
а всички останали – според уравнение (4.10.2). Вижда се още,
че от всяко ниво на конвейера окончателно се получават по две младши цифри на
произведението, а сумиращите схеми имат една и съща дължина.
В
случаите, когато дължината n на разрядната мрежа е четно число, в последната степен на
конвейера ще се събират само две числа, от което следва, че в последната степен
ще бъде употребен обикновен двоичен суматор. В случай, че дължината на
разрядната мрежа е нечетно число, тогава всички сумиращи схеми ще бъдат
еднакви.
Представената конвейерна структура може да се прилага и
за умножение на числа със знак, представени в допълнителен код. Единственото
изменение, което следва да се направи, се състои в това, че в последната степен
следва да се изпълни операция изваждане на множимото, която се налага за
корекция на произведението. Това може да бъде реализирано автоматично, чрез
управление на входния за суматора мултиплексор с помощта на знаковия бит на
множителя yn-1 в
съответствие с логиката на следния оператор
![]()
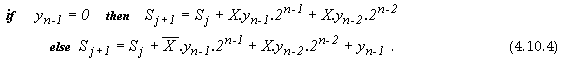
В съответствие с изложените до момента съображения,
принципната логическа схема на необходимия за конвейерното приложение
концентратор ще има вида, показан на фигура 4.10.3.
Фиг. 4.10.3. Логическа схема конвейерния концентратор
Заключение
Всички известни схеми за умножение, за
разлика от представената тук, се характеризират с използване на двоичен
суматор, в който междинната сума се събира с някакъв еквивалент на поразрядно
произведение. Този еквивалент се избира като се мултиплексира по единия от
входовете на суматора измежду няколко достатъчно сложни за получаване
резултата. Броят на тези резултати за всяко ниво в конвейера се движи от 5
нагоре. Тук имаме предвид схеми, които се получават при използване на алгоритми
поне за умножение едновременно с 2 разряда от множителя, с които е естествено
сравняваме тук предложената схема. Това означава, че апаратните разходи за
реализация на комбинационната част на всяко ниво в конвейерния умножител са
най-малко 2 пъти по-вече в сравнение с тези в тук предложената.
По същия начин стои въпросът с оценката на
бързодействието на тези схеми. От тук логично следва, че при синхронно
управление, тактовата честота за надеждно и стабилно управление на предложения
конвейер с концентартори, ще може да бъде повишена. Като имаме предвид
получената в раздел 4.2 икономия на време при превключване на концентратора от
(3.t), то
след натрупването му в умножителя, времето му за превключване ще бъде
допълнително намалено със стойност
![]()
Описаната структура
е експериментирана конкретно за синхронно умножение на 8-битови числа. Този
примерен вариант на проекта е реализиран в технологичната среда WebPack ISE на
фирма Xilinx, чрез HDL-езика Verilog, като е предназначен за имплементиране в
FPGA-матрица от фамилията Spartan II на същата фирма. На моделната
времедиаграма, показана по-долу, може да се види конвейерното умножение на
последователните двойки съмножители:
7.23=161 ; 10.22=220 ;
13.21=273 ; 16.20=320 ; 19.19=361 ; 22.18=396 .
На всеки такт от конвейера слизат посочените произведения
(вижте фигура 4.10.4). Върху изходите на входното ниво на конвейера, т.е. в
дълбочина, в десетична бройна система са представени стойностите на междинните
суми, до които е достигнало като междинна сума съответното произведение в
конвейера.
Фиг. 4.10.4. Изходни и междинни резултати в умножителя
На следващата фигура 4.10.5 е показан преходният процес на изходите на
концентратора във второ ниво на конвейера. Така, при движение на двойките
съмножители и преминаването им през това ниво, на неговия изход последователно
се получават междинните суми 20, 27, 34, 40 и 45.
Тъй като периодът на тактовата
последователност в случая е 15[ns] и ясно се вижда, че е възможно да бъде
намален двойно, то можем да твърдим, че такъв конвейер ще генерира 16-битово
произведение на всеки 7,5[ns]. С други думи повече от 133.106 числа
в секунда.
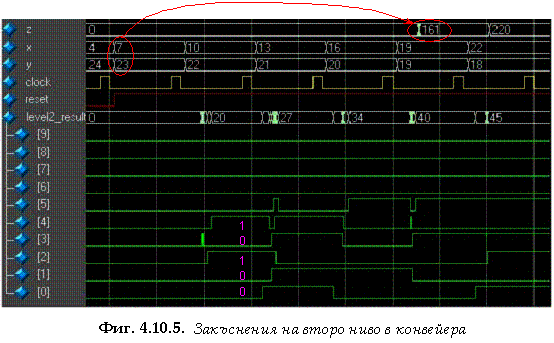
4.11.
Заключителни бележки по глава 4
В тази глава са разгледани различни подходи за повишаване
на изчислителната производителност на операционни логически схеми. Получени са
следните резултати:
1.
Синтезирана
е логическа схема на многоразряден двоичен комбинационен суматор с ускорен
последователен пренос, който е предназначен за работа в условията на асинхронен
метод за управление. За целта е синтезирана логическата функция на фактическото
закъснение (Copmlete Detection) при сумиране. За тази схема е
предложена асиметрична закъснителна верига, която минимизира апаратните разходи
на суматора с 50% при същото бързодействие;
2.
Синтезирана
и изследвана е логическа схема на многоразряден двоичен комбинационен суматор
за едновременно събиране на три операнда. Схемата е определена като
концентратор (3:1). При същите апаратни разходи схемата се характеризира с
по-малко време за превключване;
3.
Формулирана
е задача за синтез на многоразряден двоичен комбинационен суматор за събиране
на r на брой операнди (r>3). За получаване на общия вид на количествените
оценки за обема на апаратните разходи и на времето за превключване на схемата е
формулирана и доказана теорема за общия вид на оценката за максимално
възможната разрядност на сумата;
4.
Предложена е паралелна логическа структура, наречена
“хоризонтален” суматор, използваща еднобитови
концентратори (3:1). Синтезиран е алгоритъм за изчисляване на количествените
оценки на структурата при произволни параметри (брой и формат на операндите);
5.
Чрез
сравнителен анализ на възможните за суматора логически структури –
последователна, паралелна с 2-входови и паралелна с 3-входови суматори, са
направени следните изводи:
5.1. По критерия за апаратни разходи предложените
структури с паралелна организация са по-икономични с около 10%. 2-входовата и
3-входовата структури с паралелна организация не са конкурентни;
5.2. По критерия време за превключване,
предложените структури с паралелна организация са без конкуренция.
Бързодействието на паралелната структура почти не се влияе от дължината на
операндите.
6.
Предложена е нова
организация на паралелния многооперанден суматор, наречена “вертикална”. Анализът на тази организация изявява две задачи – задача
за изчисляване на битовата сума и задача за изчисляване на сумата от поразрядно
претеглените битови суми;
7.
Предложена е паралелна логическа структура, за изчисляване на
битовите суми и паралелна логическа структура за сумиране на поразрядно
претеглените битови суми, изградени с концентратори (3:1);
8.
Синтезирани
са алгоритми за оценка на за апаратните разходи и на времето за превключване на
паралелната структура. Чрез сравнителен анализ между хоризонталната и
вертикалната структури са направени два основни извода:
8.1. По критерия за апаратни разходи предложените
структури могат да бъдат признати за еквивалентни;
8.2. При еднакви крайни резултати, времето за
превключване на хоризонталната и на вертикалната структури е еднакво, докато
броят на операндите е по-голям от тяхната дължина (r>>n). При обратното
съотношение (r<<n), времето за превключване на вертикалната структура е 2
пъти по-малко от това на хоризонталната. Тези резултати могат да са подпомогнат
конструктора при избора на структура.
9.
При това изследване са получени количествени оценки за
производителността на 4 вида организации на изчислителния процес:
·
Последователно (не
конвейерно) синхронно управление;
·
Паралелно
(конвейерно) синхронно управление;
·
Последователно (не
конвейерно) асинхронно управление;
·
Паралелно
(конвейерно) асинхронно управление.
Оценките са получени в условията на предположение за
нормален закон на разпределение на закъснението при операция събиране. Това
позволява да бъдат направени и качествени сравнения. Без конкурент е
паралелната (конвейерна) асинхронна организация на управлението, която е 2 пъти
по-производително от синхронната. Сравнителните оценки са представени в таблица
4.5.1.
10.
Установено
е експериментално, че закона за разпределение на закъснението при операция
събиране, е логаритмично нормален. Така най-вероятната дължина на верижките от последователно разпространяващи се
преноси в действителност, е почти два пъти по-къса, в сравнение с
предполагаемия нормален закон на разпределение. Според експеримента,
закъснението при събира е не повече от 8-10[b]. Така оценката за
производителността на асинхронния конвейер е поне 2 пъти по-висока от
получената за нормалния закон на разпределение.
11.
Синтезирана
е логическа схема на мултиформен, мултиформатен цифров компаратор.
·
Схемата е
мултиформена, защото е инвариантна към запетаята на числа, представени в
позиционни бройни системи. Тя е инвариантна още към различните машинни кодове
(прав, обратен, допълнителен и техните модификации);
·
Схемата е
мултиформатна, тъй като е инвариантна към дължината на разрядната мрежа, в
която са представени числата, което се дължи на свойствата на инверсните
машинни кодове;
·
Схемата е
инвариантна още към кода за представяне на десетичните цифри, стига той да
притежава свойството монотонност;
·
Схемата проявява
своите универсални възможности и върху числа представени във форма с плаваща
запетая според стандарта IEEE-754;
12.
Установено
е експериментално, че закона за разпределение на закъснението при операция
сравнение с цифров компаратор е геометричния закон. Очакваното време за
превключване на компаратора е в границите на 1/3 от неговата дължина, т.е.
около 10[b] от дължината на разрядната мрежа.
13.
Предложена
е логическа структура на конвейерен схемен умножител. Синтезирана е логическата
схема на конвейерен концентратор от тип (3:1). Използването му води до алгоритъм за умножение, който е от класа на
методите за умножение с 2 разряда едновременно. В условия на асинхронен
конвейер, умножителят е по-бърз от други представители на същия клас. Получена
е аналитична оценка за спестеното време като функция от разрядността на
операндите;
Синтезираните в глава 4 логически схеми са
напълно оригинални и технически реализации с тяхно използване принадлежат на
автора.